Question

поможіть!!!

Знайдіть площу прямокутного трикутника гіпотенуза якого дорівнює 26см а один з катетів на 14 см більший за другого

Answer 1

Обозначим меньший катет как x. По теореме Пифагора имеем:

$x^2+(x+14)^2=26^2\\\\2x^2+28x+196-676=0\\\\2x^2+28x-480=0\\\\x^2+14x-240=0; \qquad x=10$

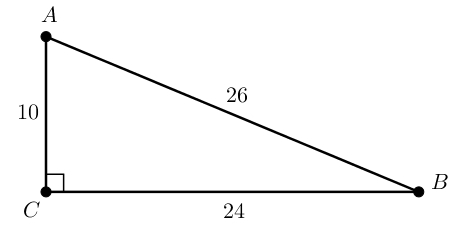
Следовательно, больший катет равен 10+14=24. Площадь прямоугольного треугольника равна полупроизведению катетов, поэтому:

$S=\dfrac{1}{2} \cdot 10 \cdot 24=120$

Ответ: 120 см².

Answer 2

Нехай один катет х см, тоді другий х+14 см.

За теоремою Піфагора 26²=х²+(х+14)².

х²+х²+28х+196-676=0

2х²+28х-480=0

х²+14х-240=0

х=10

Один катет 10 см, другий катет 10+14=24 см.

S=1\2 * 10 * 24 = 120 cм²