Предмет: Алгебра,
автор: HNLLZ
|-х²-х|≥4х-2
Помогите, пожалуйста, решить неравенство
Ответы
Автор ответа:
1
Решение на фотографии
Приложения:

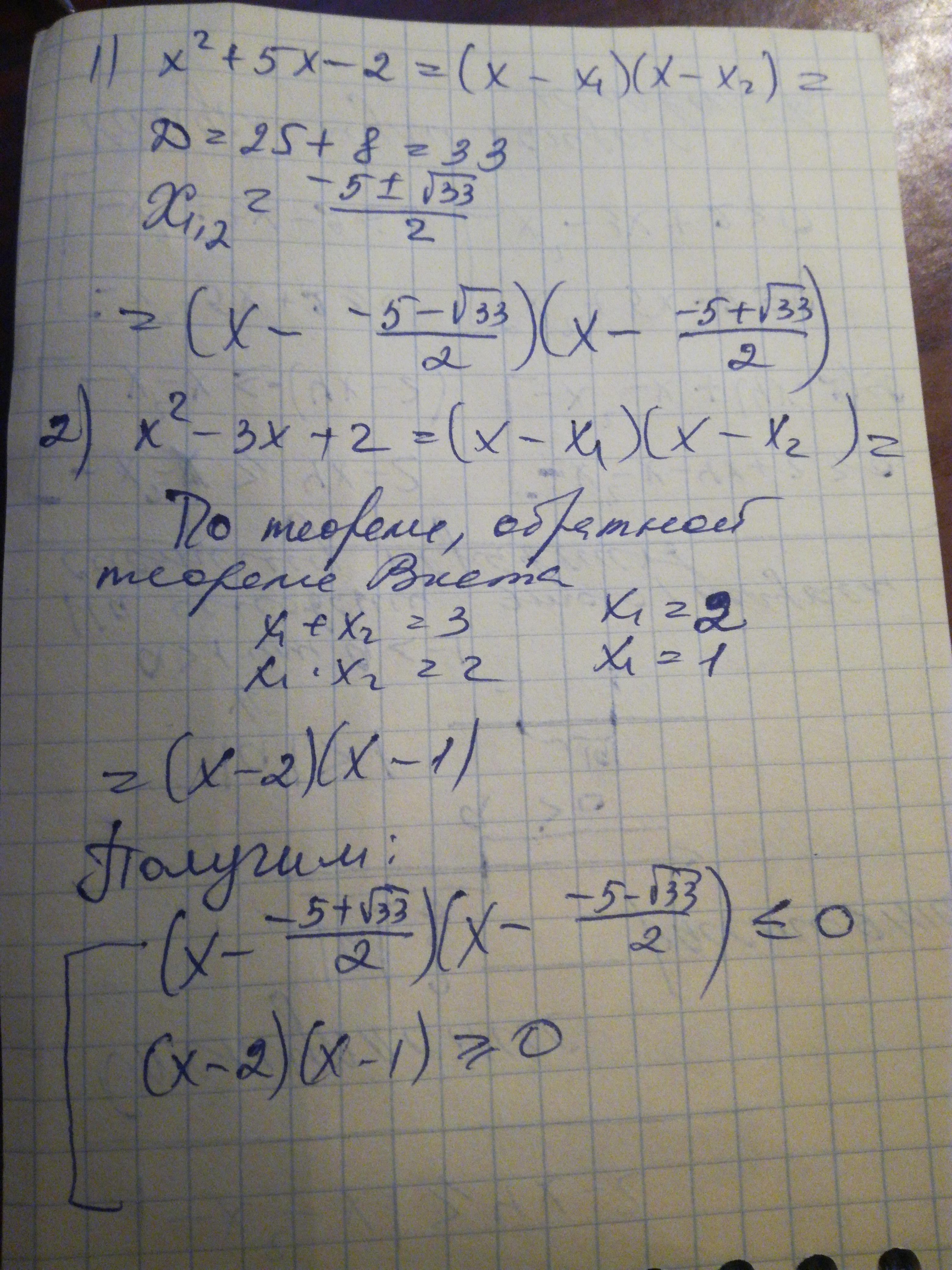

HNLLZ:
Спасибо!
Автор ответа:
1
task/29824203 решить неравенство | - x² - x | ≥ 4x - 2
решение | - x² - x | ≥ 4x -2 ≡ | x² +x | ≥ 4x -2 , т.к. | - x² - x | = |-(x²+x | = | x² + x |
а) Любое значение переменного при котором 4x -2 ≤ 0 , т.е. x ≤ 1/2 является решением неравенства . x ∈ ( -∞ ; 1/2 ] . (1)
б) x > 1/2 ; x² + x > 0 ⇒| x² + x | = x² + x , поэтому x² + x ≥ 4x -2
x² -3x +2 ≥ 0 ⇔(x - 1)(x - 2) ≥ 0 + + + + + [1] - - - - - [2] + + + + + +
x ∈ (1/2 ; 1 ] ∪ [ 2 ; +∞ ) . (2)
ответ : x ∈ (∞ ; 1] ∪ [ 2 ; +∞).
* * * P.S. ( -∞ ; 1/2 ] ∪ (1/2 ; 1] ∪ [2 ; +∞) = (- ∞ ; 1 ] ∪ [2 ; + ∞) * * *
Удачи !
Похожие вопросы
Предмет: Математика,
автор: brawlstars205001
Предмет: Математика,
автор: wqwhq3
Предмет: Информатика,
автор: shexrozobragimov
Предмет: Математика,
автор: дашуля199
Предмет: Математика,
автор: Валька121