Предмет: Математика,
автор: Юля3
Ребята, выручайте! Без Вас никак!
Помогите разобраться в теме
Решите и подробно распишите!
Любую задачку, любое количество!
За отдельную благодарность можете Всё, хочу на ваших решениях понять тему и научиться решать эти тяжки задачи! Надеюсь на Вас!
Заранее огромное спасибо!
Помоги :)
Приложения:
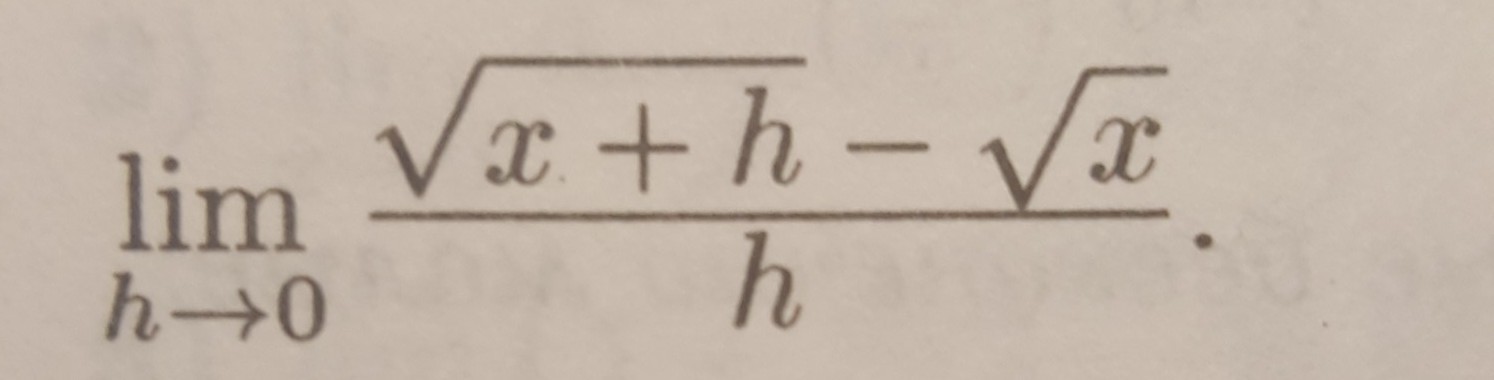
Ответы
Автор ответа:
1
Автор ответа:
1
Избавляемся от иррациональности в пределе и сокращаем на общие множители.
lim h->0 1/(√x+h +√x)=
Возьмем предел каждого члена.
lim 1 h->0√lim x h->0+lim h h->0 +lim x h->0=
Определяем пределы, подставляя 0 вместо всех вхождений h.
1/(√x+0 +√x)=1/(2√x)
Похожие вопросы
Предмет: Биология,
автор: chebypellkaa
Предмет: Другие предметы,
автор: svetlanagrigoreva039
Предмет: Английский язык,
автор: almansurab
Предмет: История,
автор: romaxa09
Предмет: Алгебра,
автор: Daniil1002