Даю 100 балов. Ребята помогите пожалуйста прошу. Теорема Безе:Докажите что многочлен F(x)делиться нацело на многочлен P(x) Если:
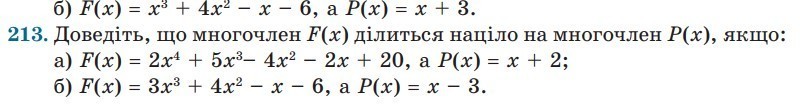
Ответы
a)
F(x)=2x⁴+5x³-4x²-2x+20
P(x)=x+2
x+2=x - (- 2) => a= - 2
По теореме Безе остаток от деления F(x) на P(x) равен F{- 2).
F(-2) = 2·(-2)⁴+5·(-2)³-4·(-2)²-2·(-2)+20 =
= 2·16 - 5·8 - 4·4 + 2·2 + 20 =
= 32 - 40 - 16 + 4 + 20 = 0
Если F(-2) = 0, то это означает, что остаток равен нулю, следовательно, многочлен F(x)=2x⁴+5x³-4x²-2x+20 делится на P(x) = x+2 без остатка.
Ответ: многочлен F(x)=2x⁴+5x³-4x²-2x+20 делится на P(x) = x+2 без остатка.
б)
F(x)=3x³ + 4x²- x - 6
P(x)=x - 3
x - 3 => x=3
F(3) = 3·3³ + 4·3²- 3 - 6 = 81 + 36 - 3 - 6 = 108
Oстаток F(3) ≠0, следовательно, многочлен F(x)=3x³ + 4x²- x - 6 делится на P(x) = x-3 c остатком.
Ответ: многочлен F(x)=3x³ + 4x²- x - 6 делится на P(x) = x-3 c остатком, равным 108.
б) верхний
F(x) = x³ + 4x²- x - 6
P(x)=x + 3
x - (-3) => x= - 3
F(- 3) = (-3)³ + 4·(-3)²- (-3) - 6 = - 27 + 36 + 3 - 6 = 6
Oстаток F(3) ≠0, следовательно, многочлен F(x)=x³ + 4x²- x - 6 делится на P(x) = x+3 c остатком.
Ответ: многочлен F(x) = x³ + 4x²- x - 6 делится на P(x) = x+3 c остатком, равным 6.