Предмет: Алгебра,
автор: Simba2017
Как найти предел? (Вопрос не для всех)
Приложения:
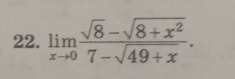
Ответы
Автор ответа:
1
При нахождении предела возникает неопределенность (0/0), которую необходимо раскрыть. Здесь можно поступать разными способами, но проще всего использовать правило Лопиталя: если вычисление предела отношений двух бесконечно малых или бесконечно больших функций даёт неопределённости видов 0/0 или ∞/∞, то предел отношения двух функций можно заменить пределом отношения их производных и, таким образом, получить определённный результат.
Найдем эти производные. Пусть
Тогда производная этой функции:
Рассуждая аналогичным образом, получаем для знаменателя:
Применяем правило Лопиталя:
Ответ: 0.
Похожие вопросы
Предмет: Английский язык,
автор: Fmdd
Предмет: Английский язык,
автор: samuratmullabaev
Предмет: Математика,
автор: kilindilsat3
Предмет: Биология,
автор: юля1046
Предмет: Математика,
автор: таня2113