Предмет: Математика,
автор: golovachevkonstantin
Вычислить площадь фигуры, ограниченной линиями
Ответы
Автор ответа:
1
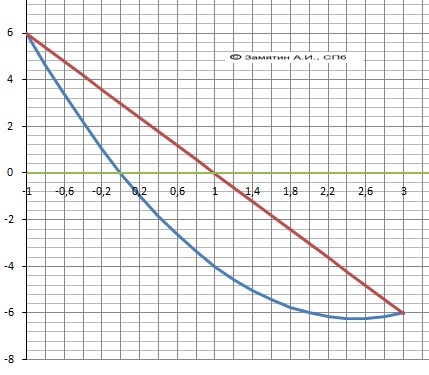
Пределы интегрирования: х² - 5*х = 3 - 3*х, a = 3, b = -1
Площадь фигуры - интеграл разности функций.
Рисунок с графиками в приложении.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Литература,
автор: toty29102010
Предмет: История,
автор: Аноним
Предмет: Математика,
автор: донут
Предмет: Математика,
автор: катуахелп