докажите,что не являются тождественно равными выражения
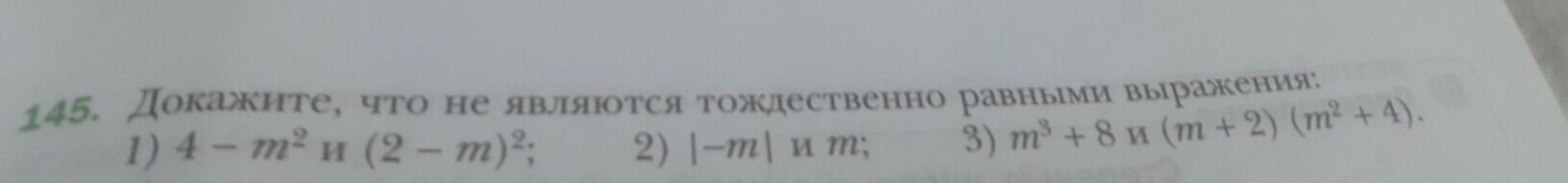
Ответы
Ответ:
Выражения являются тождественно равными, если они выполняются для всех значений переменных.
Значит, чтобы доказать, что выражения не являются тождественно равными достаточно найти хоть одно значение переменного для которого равенство не выполнено.
1) Рассмотрим выражения 4-m² и (2-m)². Предположим, что выражения равны:
4-m² = (2-m)² ⇔ 4-m² = 4-4·m+m² ⇔ 2·m² - 4·m = 0 | :2 ⇔
⇔ m² - 2·m = 0 ⇔ m·(m-2) = 0 !
Последнее равенство означает, что выражения равны только при m=0 или m=2, а для остальных значений m не равны. Это доказывает, что выражения не являются тождественно равными.
2) Рассмотрим выражения |-m| и m. Из определения модуля получаем
.
Предположим, что выражения равны: |-m| = m.
Тогда при m<0: |-m| = m ⇔ m = m ⇔ 0 = 0,
а при m≥0: |-m| = m ⇔ -m = m ⇔ 2·m = 0 ⇔ m = 0 !
Последнее равенство означает, что выражения равны только при m=0, а для остальных значений m> не равны. Это доказывает, что выражения не являются тождественно равными.
3) Рассмотрим выражения m³+8 и (m+2)·(m²+4). Предположим, что выражения равны:
m³+8 = (m+2)·(m²+4) ⇔ m³+8 = m³+2·m²+4·m+8 ⇔ 2·m² + 4·m = 0 | :2 ⇔
⇔ m² + 2·m = 0 ⇔ m·(m+2) = 0 !
Последнее равенство означает, что выражения равны только при m=0 или m= -2, а для остальных значений m не равны. Это доказывает, что выражения не являются тождественно равными.