Предмет: Алгебра,
автор: enotik149
помогите пожалуйста с задание :1 с расписанием действий
Приложения:
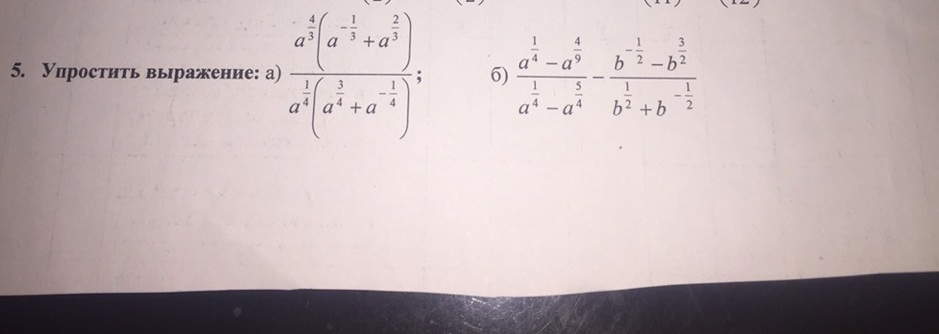
NNNLLL54:
в условии б) описка: вместо а^{9/4} написали a^{4/9}...
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Информатика,
автор: iross7167
Предмет: Математика,
автор: makcem63
Предмет: Другие предметы,
автор: Аноним
Предмет: Математика,
автор: nevi98