Предмет: Математика,
автор: uinvfjndvhdnfhv
Вычислить пределы......................................................:
Приложения:

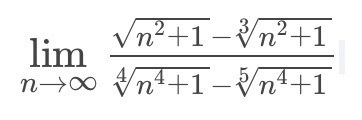
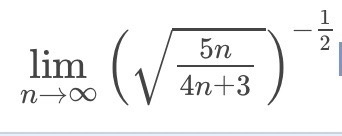
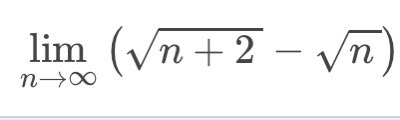
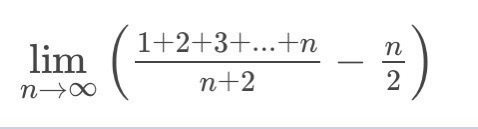
Ответы
Автор ответа:
0
1)
2)
3)
4) Тут у нас неопределённость вида либо , либо
5)
Похожие вопросы
Предмет: Қазақ тiлi,
автор: Dghdbdv
Предмет: Алгебра,
автор: veronikagovzan85
Предмет: Русский язык,
автор: gyggyyyg9
Предмет: Математика,
автор: Муся205
Предмет: Математика,
автор: влад1023