Question

Из точки ,взятой на одной из сторон равностороннего треугольника ,проведены 2 прямые ,параллельные другим его сторонам .определите вид получившегося четырехугольника и все его углы

Answer 1

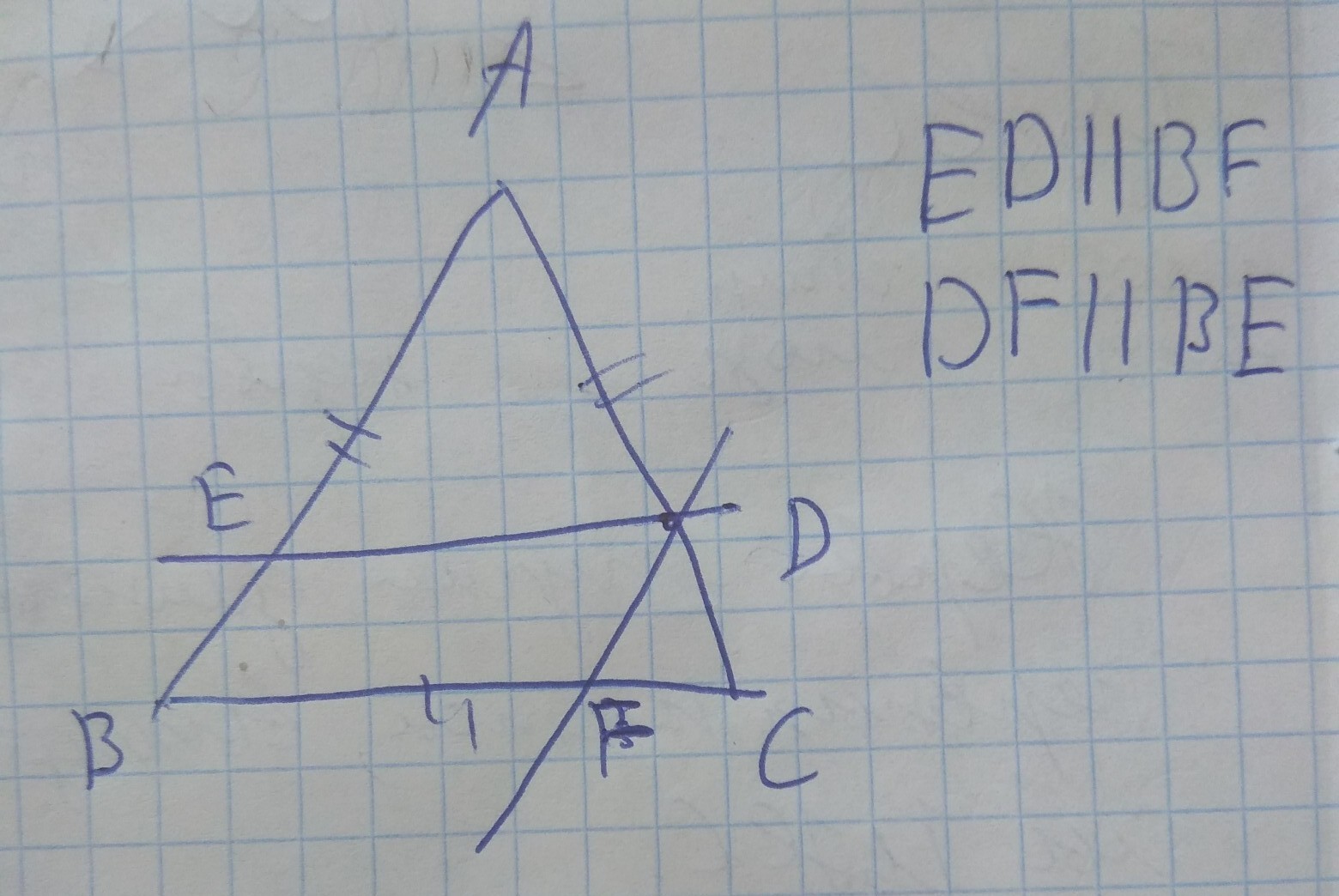
Получится параллелограмм (BEDF) . Углы 60, 60, 120, 120.
ED||BF по построению.
DF||EB по построению.
Четырехугольник у которого противоположные стороны попарно параллельны является параллелограммом.
У параллерограмма противоположные углы равны. Угол B равен 60°, т. к. это угол равностороннего треугольника (180 : 3 = 60). Угол EDF = B = 60.
Сумма углов четырехугольника равна 360°. BED = BFD. BED + BFD = 360 - EDF - B = 240
BED = BFD = 240 : 2 = 120.

Answer 2

Это паралеллограмм угол СDE=60°; DCB=120°; CBA=60°; BAD=120°