Решить уравнение не используя графический метод.
Вариант решения через систему а-ля "каждое слагаемое равно нулю" уже пробовал:

Но корней должно быть как минимум 3.
Ответы
Заменим синус на ряд до х^5.
sin(x) = x - (x^3/6) + (x^5/120) = (120x -20x^3 + x^5)/120.
Тогда исходное уравнение примет вид:
x^3 = (120x -20x^3 + x^5)/120.
Получаем x^5 - 140x^3 + 120x = 0.
Вынесем х за скобки: х(x^4 - 140x^2 + 120) = 0.
Отсюда имеем один корень: х = 0.
Второй множитель преобразуем в квадратное уравнение при помощи замены x^2 = t.
t² - 140t + 120 = 0.
Квадратное уравнение, решаем относительно t:
Ищем дискриминант:
D=(-140)^2-4*1*120=19600-4*120=19600-480=19120;
Дискриминант больше 0, уравнение имеет 2 корня:
t_1=(√19120-(-140))/(2*1)=(√19120+140)/2=√19120/2+140/2=√19120/2+70 ≈ 139.137544069775 (этот корень даёт отрицательное значение синуса, тогда как куб - положительное)
t_2=(-√19120-(-140))/(2*1)=(-√19120+140)/2=-√19120/2+140/2=-√19120/2+70 ≈ 0.8624559302255.
х = √t = √0.8624559302255 = +-0,928685054
.
Если взять более длинный ряд разложения синуса, то получим значение:
х = +-0,928626.
Ответ: имеем 3 корня: х = 0 , х = 0,928626 и х = -0,928626.
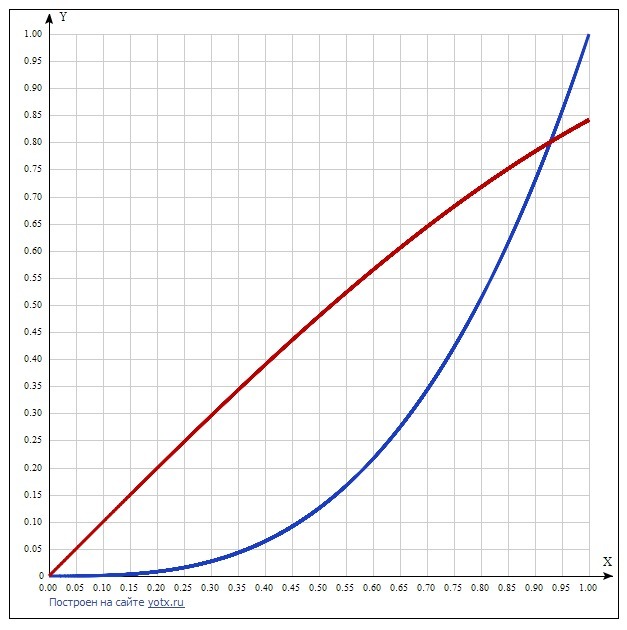
Для наглядности приводится график функций х^3 и sin(x) в пределах от 0 до х.
.