Решите иррациональное уравнение
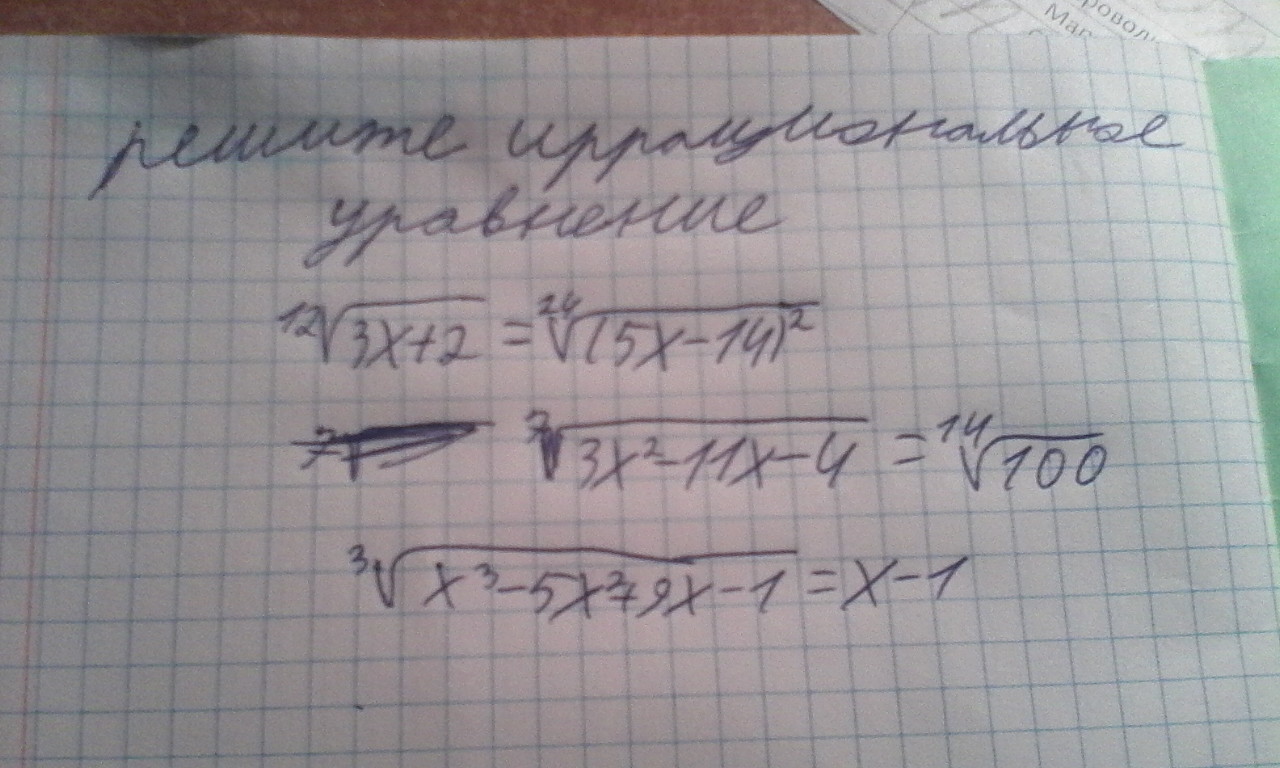
Ответы
Решение.
1)
ОДЗ.
(5х - 14)² ≥ 0 при любых х
3х + 2 ≥ 0; 3х ≥ - 2; х ≥ -2/3
х∈[-2/3; +∞)
Возводим левую и правую части уравнения в 24-ю степень.
(3х + 2)² = (5х - 14)²
9х² + 12х + 4 = 25х² - 140х + 196
16х² - 152х + 192 = 0
2х² - 19х + 24 = 0
D = 19² - 4 · 2 · 24 = 169
√D = 13
x₁ = (19 - 13)/4 = 1.5
x₂ = (19 + 13)/4 = 8
Проверка x₁ = 1.5
Проверка x₂ = 8
Ответ: x₁ = 1.5; x₂ = 8
2)
ОДЗ:
Поскольку > 0, то и 3х² - 11х - 4 > 0
3х² - 11х - 4 = 0
D = 11² + 4 · 3 · 4 = 169
√D = 13
x₁ = (11 - 13)/6 = -1/3
x₂ = (11 + 13)/6 = 4
Неравенство 3х² - 11х - 4 > 0 имеет решение х∈(-∞; - 1/3)∪(4; +∞)
То есть ОДЗ: х∈(-∞; - 1/3)∪(4; +∞)
Возводим левую и правую части уравнения в 7-ю степень
3х² - 11х - 4 = 10
3х² - 11х - 14 = 0
D = 11² + 4 · 3 · 14 = 289
√D = 17
x₁ = (11 - 17)/6 = -1
x₂ = (11 + 17)/6 = 14/3 =
Проверка x₁ = -1
Проверка x₂ = 14/3 =
Ответ: x₁ = -1; x₂ =
3)
ОДЗ: х∈(-∞; +∞)
Возводим правую и левую части уравнения в 3-ю степень
х³ - 5х² + 9х - 1 = (х - 1)³
х³ - 5х² + 9х - 1 = х³ - 3х² + 3х - 1
-5х² + 9х = -3х² + 3х
2х² - 6х = 0
2х (х - 3) = 0
х₁ = 0
х₂ = 3
Проверка х₁ = 0
-1 = -1
Проверка х₂ = 3
2 = 2
Ответ: x₁ = 0; x₂ = 3