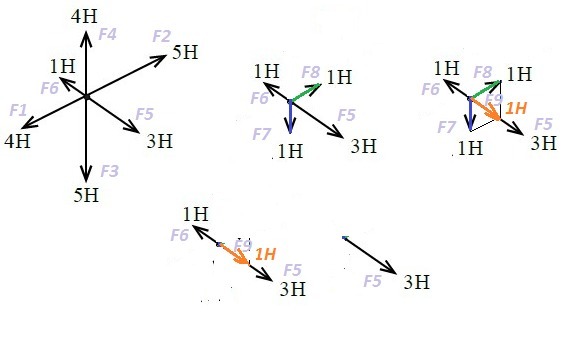
Шесть сил приложены к одной точке плоскости, так что углы между соседними силами равны
60∘ (см. рис. 53). Найти модуль равнодействующей этих сил.
Ответы
выходит надо сложить три цветных вектора....
Дано : F₁ = 4H; F₂=5H; F₃=5H; F₄=4H; F₅=3H; F₆=1H
Углы между соседними силами равны 60°
Будем искать равнодействующую, складывая векторы сил последовательно.
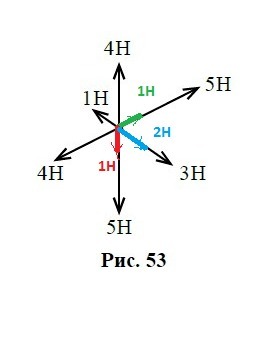
Силы и
направлены в противоположные стороны вдоль одной линии, поэтому их равнодействующая равна разности сил и направлена в сторону большей силы
.
; F₈=5H - 4H = 1H
Аналогично, ; F₇=5H - 4H = 1H
Силы и
складываем по правилу параллелограмма, который в данном случае является ромбом (F₇=F₈=1H). Поэтому вектор суммы является меньшей диагональю ромба и равен стороне ромба, так как острые углы ромба равны по 60°.
; F₉=1H
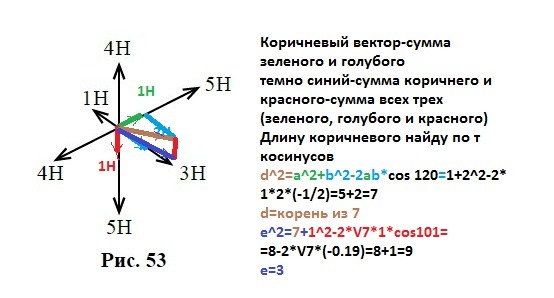
Векторы и
направлены вдоль одной прямой в разные стороны и равны по 1Н, поэтому их равнодействующая равна нулю.
Осталась только сила - она и будет равнодействующей шести сил. Следовательно, модуль равнодействующей равен модулю силы
, то есть равен 3Н.