Предмет: Алгебра,
автор: bnoe3de
Решите пожалуйста уравнения. Желательно подробно.
Приложения:
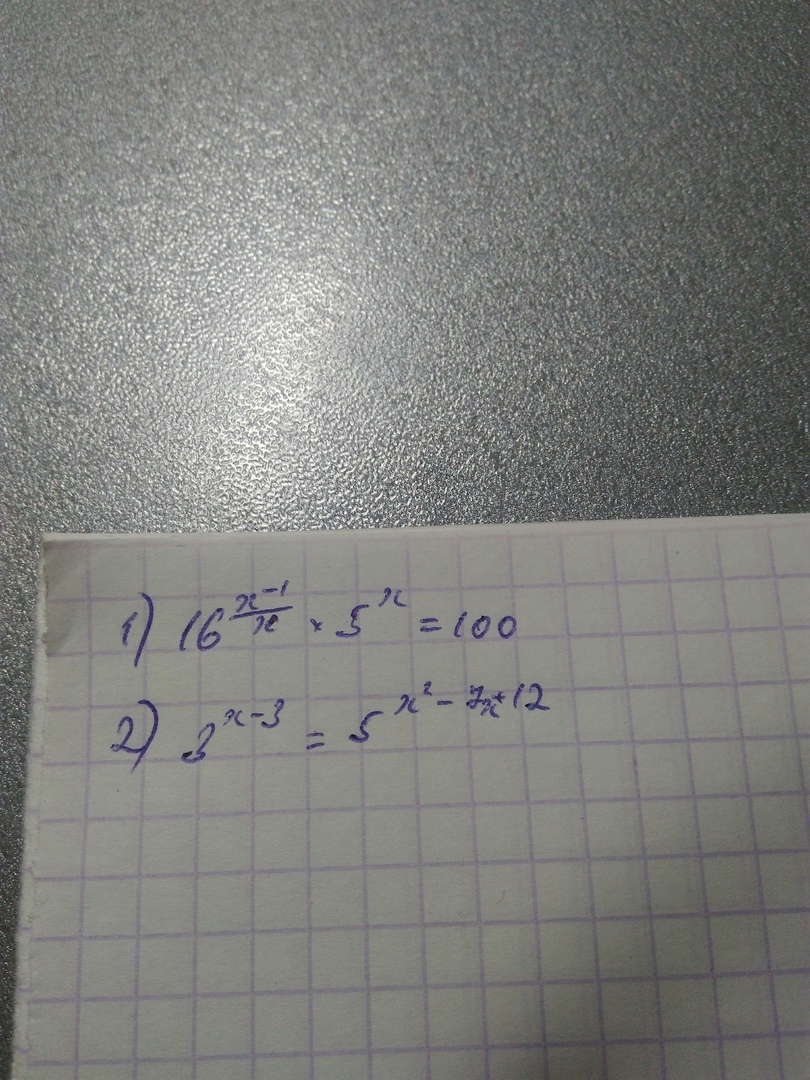


csharp:
Сомневаюсь, что они решаются. Проверь, правильно ли ты списал.
степень 16 какая? (x-1)/x ? 5 в степени x?
во-втором уравнении 3 или 5 в степени (x-3) что за ужасный почерк?)
я сейчас сделаю лучше.
Это ещё нормальный)))))))
Я добавил 2 фотографии в цифровом виде.
1 уравнение) странно в тетради 100 в конце, на фотке 10 )))
это я дурак))
там 100
там 100
В первом, полагаю, нужно прологарифмировать. Ответ x = 2. Решать я не осмелюсь, конечно же.
Да, просто в photomath перепиши пример, взяв всё в десятичный логарифм. log_10(...) = log_10(100)
Ответы
Автор ответа:
2
Ответ. 1) ; 2)
Не устал?) Молодец.
Устал)
не я сдался когда увидел что дискриминант будет на полстраницы формул. рука опухнет ;(
Похожие вопросы
Предмет: Химия,
автор: naskinakaram
Предмет: История,
автор: serdukovav54
Предмет: Алгебра,
автор: galinaragimova27
Предмет: Математика,
автор: иооолл
Предмет: Математика,
автор: Mederbek