В одном детском садике было ровно 20 детей и каждый из них дружил с каждым из остальных. Кикимора и старуха Шапокляк решили посоревноваться в умении делать пакости. Они по очереди ходят в садик (первая - Кикимора) и ссорят пару детей друг с другом, из-за чего те перестают дружить. Проиграет тот, кто оставит кого-либо из детей совсем без друзей. Как старухе Шапокляк обыграть Кикимору при любых действиях Кикиморы?
Ответы
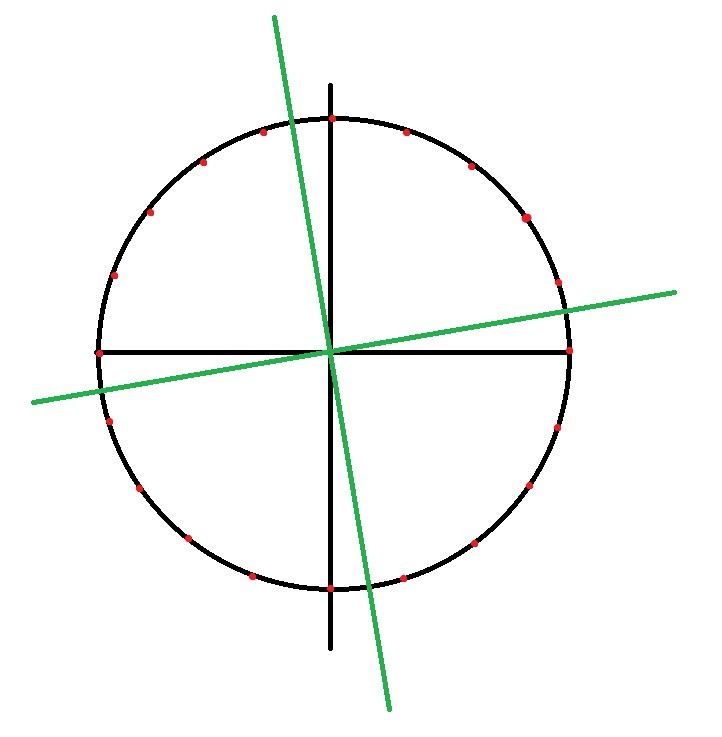
расставим детей на окружности так, чтобы получился правильный 20-тиугольник. (на рис). Тогда, чтобы выиграть, Шапокляк должна делать ходы симметричные относительно центра окружности. т.е. находить точки диаметрально противополжные точкам Кикиморы. Если же Кикимора убирает диагональ, которая образует диаметр, то Шапокляк должна убрать диаметр который симметричен относительно зеленой оси (любой из, выбрать одну)Рассмотрим в нем зеленую ось ближе к вертикальной, (но на деле можно любую из них). После каждого хода Шапокляк будет оставаться картинка симметричная относительно центра окружности. Что означает, что если после ее хода образуется висячая вершина, то значит, такая была и после хода Кикиморы. Значит, Шапокляк при такой игре всегда выиграет