Предмет: Алгебра,
автор: ОлЭнь09
Решите неравенство:
x^4+5x^3+10x^2+20x+24>0
Ответы
Автор ответа:
0
Разложим левую часть неравенства на множители
Третий множитель очевидно, что , поэтому достаточно решить неравенство
___+____(-3)____-___(-2)___+____
Ответ: x ∈ (-∞; -3) ∪ (-2; +∞).
Автор ответа:
0
Ответ:
Объяснение:
Сначала решим уравнение четвертой степени.
По теореме Безу его корни надо искать среди делителей свободного члена (в нашем случае свободный член равен 24)
Простым подбором, получаем 2 корня:
x = -2 и x= -3
Далее найдем произведение:
(x+2)·(x+3) = x² + 5x + 6
Разделим исходное уравнение на полученное произведение "столбиком"
Итак, неравенство можно написать так:
(x+2)(x+3)(x²+4) > 0
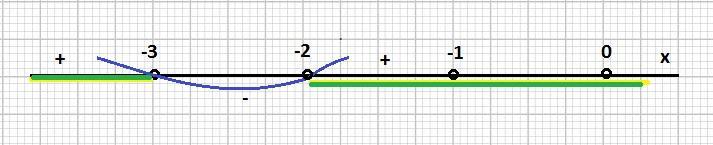
Поскольку (x²+4)>0, то по правилу интервалов находим решение неравенства:
(x+2)(x+3)>0
Получили:
x ∈ (-∞; - 3) ∪ (-2; +∞)
Приложения:
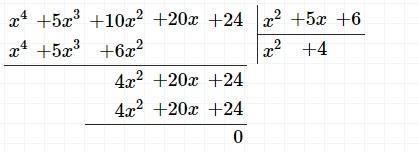
Похожие вопросы
Предмет: Қазақ тiлi,
автор: fccdvdgvh
Предмет: Українська мова,
автор: albinapropvp123
Предмет: Английский язык,
автор: Zahar5052007
Предмет: Математика,
автор: Lera0106