Предмет: Математика,
автор: k43ff
сделать лимит
правильный ответ 0
Приложения:
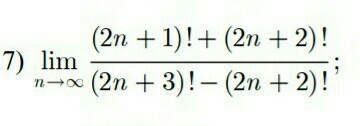
Ответы
Автор ответа:
0
edenikaev:
Отправил решение.
Похожие вопросы
Предмет: География,
автор: anadmutruc123
Предмет: Английский язык,
автор: morozovamaria581
Предмет: Алгебра,
автор: sjjejj
Предмет: Экономика,
автор: leragalkina98