Предмет: Алгебра,
автор: Бульдок111
решите пожалуйста 4 задание
Приложения:
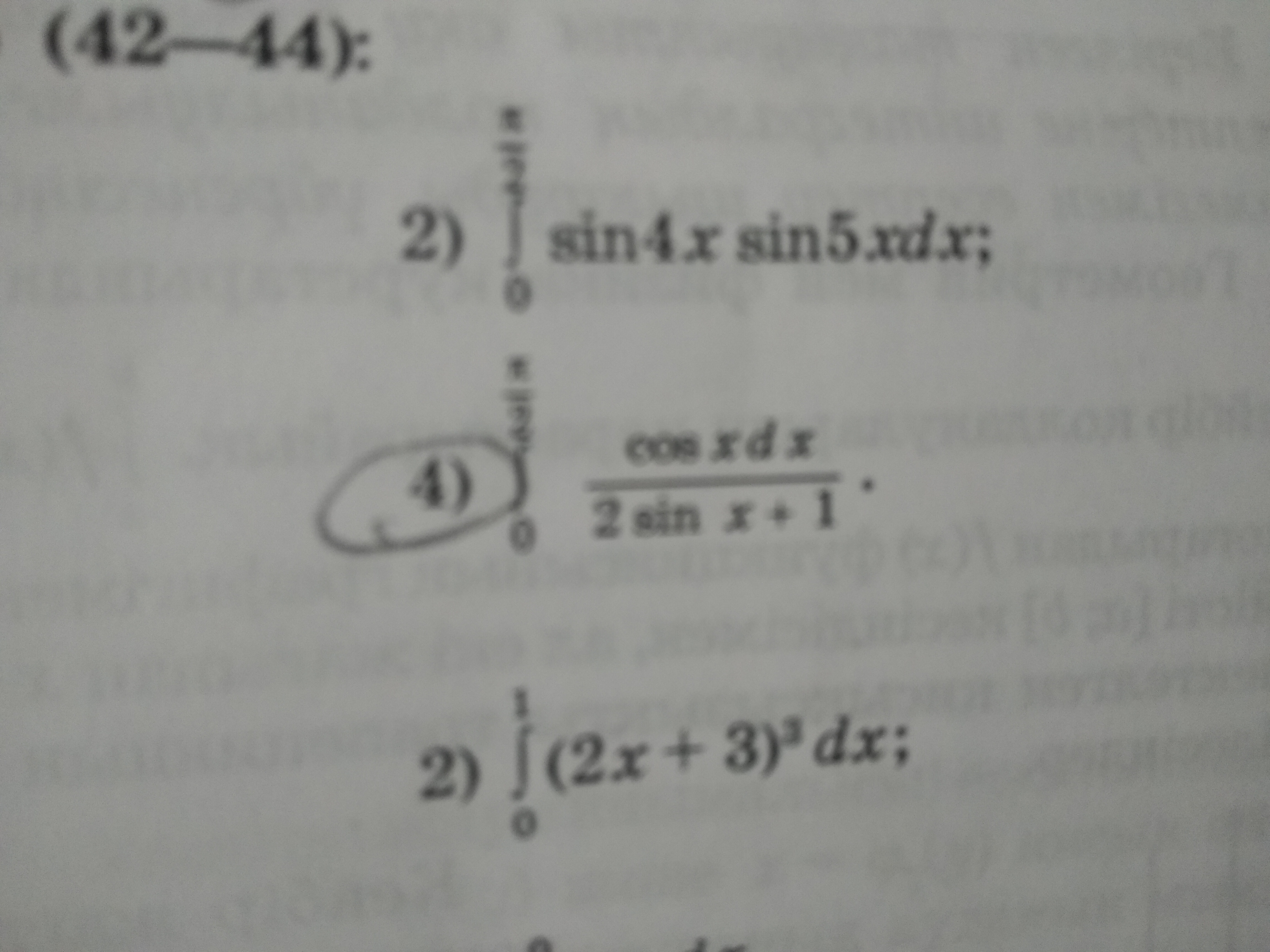
Ответы
Автор ответа:
1
Т.к

Заменим 2sinx+1 на t
Получится

Постоянное значение можно вынести за знак интеграла,под знаком интеграла получится

Интегрируем и получаем :

Теперь подставляем значения:

Заменим 2sinx+1 на t
Получится
Постоянное значение можно вынести за знак интеграла,под знаком интеграла получится
Интегрируем и получаем :
Теперь подставляем значения:
Похожие вопросы