Предмет: Алгебра, автор: bumomopile

Найдите все числа, которые при делении на 3 дают остаток 1, а при делении на 5 дают остаток 3.
Ответ запишите в виде формулы, используя неизвестную "n".
Например, все чётные числа: "2n".Например, числа, которые при делении на 5 дают остаток 3: "5n+3". И объясните.

bumomopile: За ответ спасибо, но как ты его получил? Формула, правило? Или подбор?

antonovm: решение

bumomopile: Что решение, не понял. Можешь объяснить, как ты это получил.

antonovm: могу , через минут 10 опубликую решение

bumomopile: Окей, я не тороплюсь. Спасибо

antonovm: только в конце надо исправить -t входит в Z

bumomopile: Я глупенький наверное, а можешь расписать текстово?) хотя бы после 4 строчки, а то t вводится, не пойму( за 15 баллов-то)

bumomopile: C объяснениями я имею в виду

antonovm: 3(k-4)-5(m-2)=3k-5m-2

antonovm: 3(k-4) делится на 5 , значит на 5 делится к-4 => k-4=5t

Ответы

Автор ответа: antonovm

.........................................................................................

Приложения:

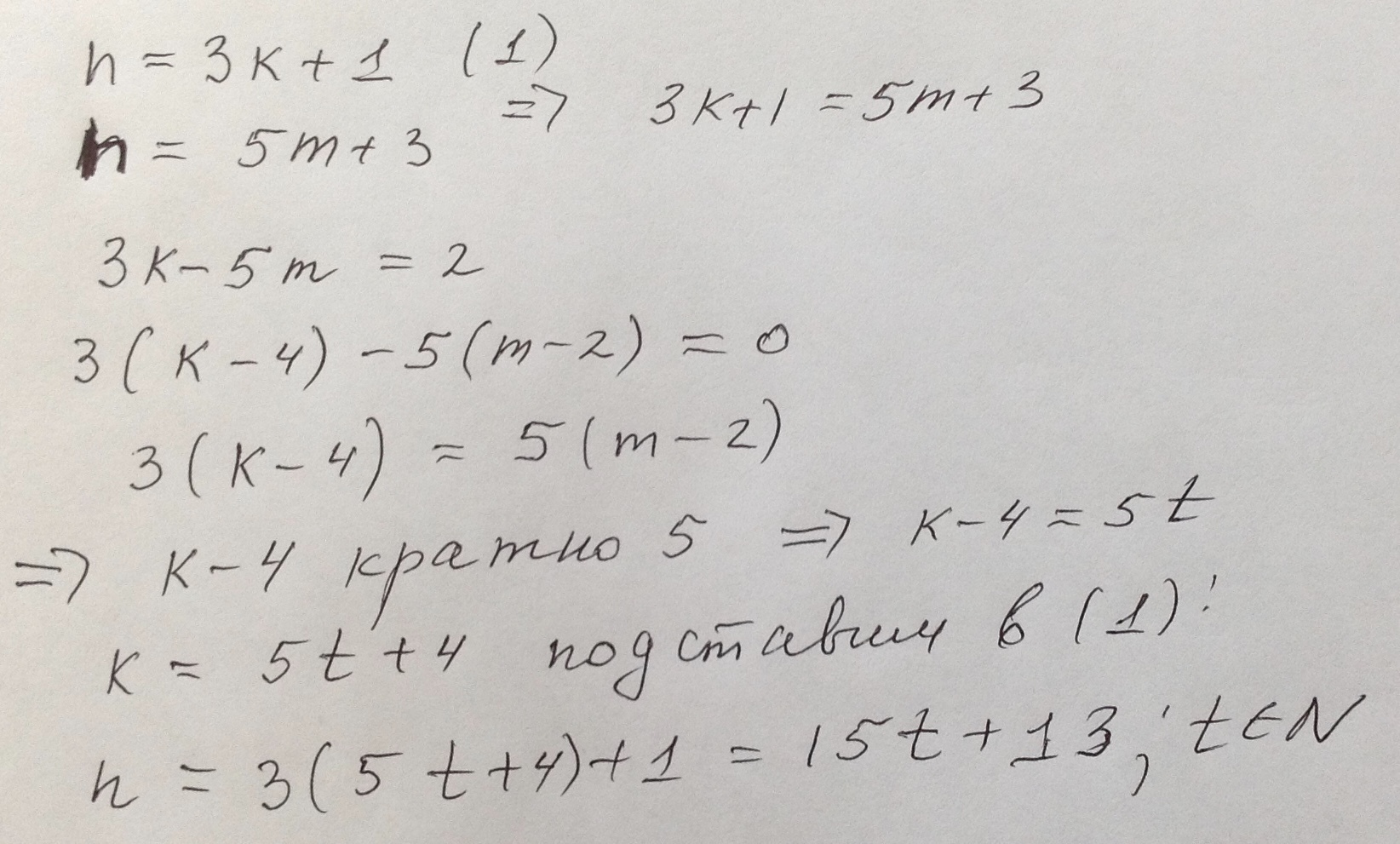
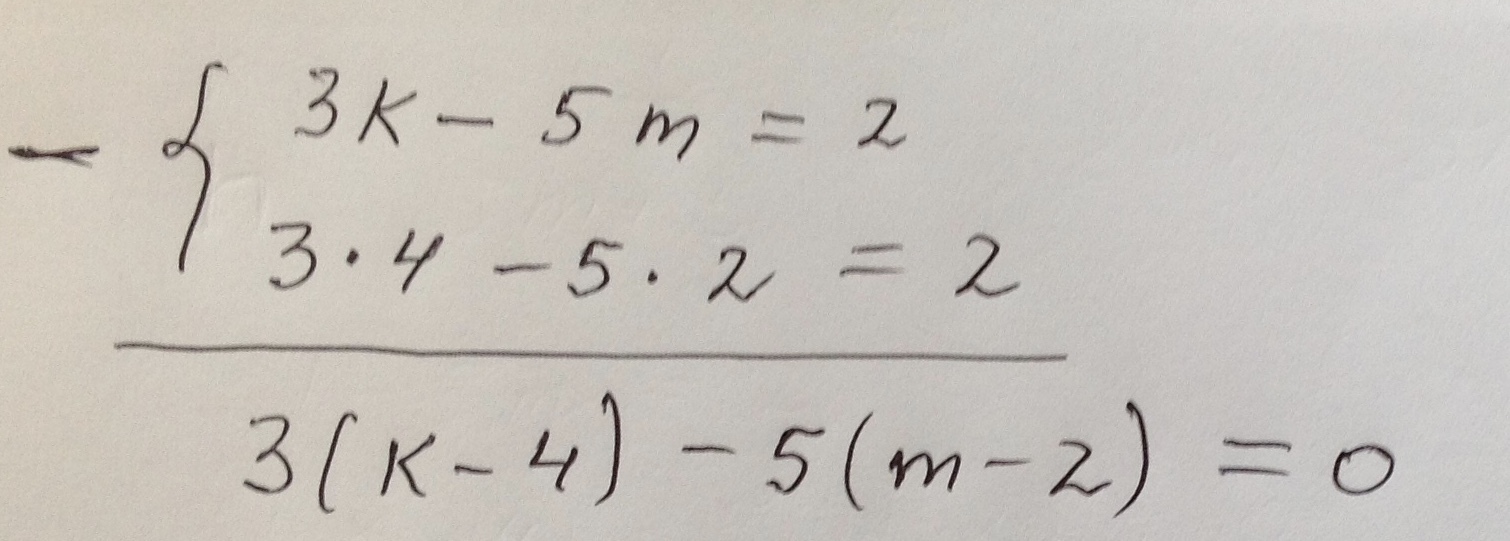
bumomopile: Можешь 4 строчку объяснить?

antonovm: 4 строчка и 3 это одно и тоже ( раскройте скобки)

antonovm: кстати , мой ответ и Зинаиды одинаковы ( одно и то же множество, но записано по разному)

antonovm: n=5m+3 (опечатка во 2 строчке)

bumomopile: ага, а то что то я запутался)

bumomopile: Вообщем спасибо. Хоть мне больше понятен был ответ Зинаиды, но за старанее спасибо)

bumomopile: старание*

antonovm: происхождение 4 строчки ( добавил лист)

Автор ответа: zinaidazina

1) Составим ряд чисел, которые при делении на 5 дают остаток 3:

8; 13; 18; 23; 28; 33; 38; 43; 48; 53; 58; ....; 5n+3;....

2) Выберем из них те числа, которые при делении на 3 дают остаток 1:

13; 28; 43; 58; ...; 15n-2;...

Ответ: 15n-2;

Предыдущий вопрос

Следующий вопрос

Похожие вопросы

Предмет: Английский язык, автор: leylaquliyeva322

Помогите пожалуйста очень срочно

6 лет назад

Предмет: Английский язык, автор: dmitry8159

Текст констатирующей работы
Jason’s Working Day (Test Booklet Module 6 p. 51)
My neighbour Jason is a baker. He is very busy. When he’s not at the bakery, he’s out having fun. Every day Jason wakes up at 5 o’clock in the morning. He has breakfast and then he rides his bike to the bakery. When he gets there, he starts to make bread. His work is very hard. He works until 3 o’clock in the afternoon. Then he goes back home where he has lunch and rests for a while. In the evenings he sometimes goes to the cinema or meets his friends. On Wednesdays he always does the shopping. On Sundays he always wakes up late and then reads a book or works in the garden. He usually goes to bed at 11 o’clock at night.

1. Choose the right variant:
1. Where does Jason work? a) at school b) at the bakery c) in the hospital
2. What time does he wake up every day? a) at 3 o’clock b) at 11 o’clock c) at 5 o’clock
3. How does he get to work? a) by bike b) by bus c) on foot
4. What time does he finish work? a) at 3 o’clock b) at 11 o’clock c) at 5 o’clock
5. When does he do the shopping? a) on Sundays b) on Wednesdays c) on Mondays
6. What does he do on Sundays? a) reads a book and plays football b) reads a book and does the shopping c) reads a book and works in the garden

2. Are the sentences True (T), False (F) or Not Stated (N)
1. Jason is a driver.
2. Jason finishes his work at three o’clock.
3. In the evenings, he goes to the cinema or meets his friends.
4. On Saturdays he always visits his granny.
5. On Wednesdays he usually plays football.
6. He goes to bed at 11 o’clock at night.

3. Answer the questions.
1. When do you usually get up?
2. What do you usually do after school?
3. Do you sometimes go to the cinema at the weekends?

6 лет назад

Предмет: География, автор: zizizizipiggi

Ребятки помогите с тестом даю 50 баллов
Ответить на тест (письменно)
1.70% ложе океана занимают:
а) котловины;
б) желоба;
в) срединно-океанические хребты.
2. Единая система горных сооружений на дне океана это:
а) материковый склон;
б) срединно-океанические хребты;
в) желоба.
3. Часть материка, продолжающегося под водой в виде мелководной прибрежной равнины это:
а) ложе океана;
б) материковый склон;
в) шельф.
4. Самые глубокие участки мирового океана – это:
а) желоба;
б) материковый склон;
в) котловины.
5. Самая глубокая впадина Мирового океана называется:
а) Филиппинский желоб;
б) Марианский желоб;
в) Зондский желоб.
6. Самые маленькие глубины Мирового океана наблюдаются:
а) на ложе океана;
б) в желобах;
в) на материковой отмели.
Ответы к тесту
1
2
3
4
5
6
А
Б
В
А
Б
В