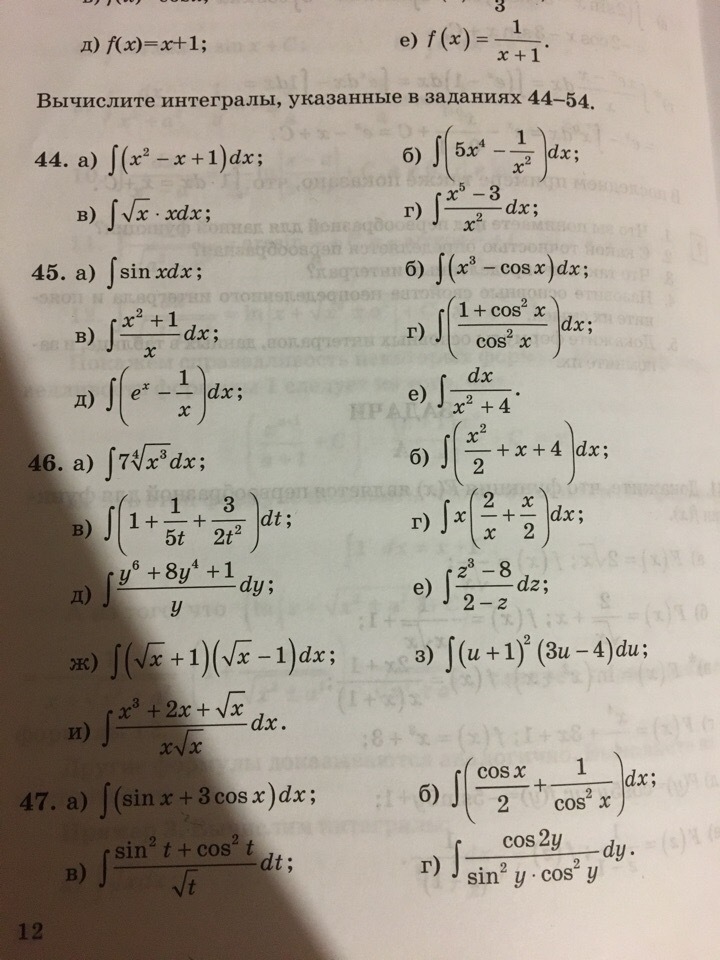46(е,з)
47(б,г)
..............................
Приложения:
Ответы
Похожие вопросы
1. Укажите предложение с обстоятельственным придаточным места. 1) Весь следующий день Сенька просидел у входа в палатку и смотрел туда, где рвутся бомбы. 2) Рота, где служил Рябинкин, заняла оборону на обширной заболоченной пойме. 3) В избе, куда их пустили пообедать, было сорно и душно, пахло хлебом и шинкованной капустой. 5. 4) Миша выскакивал на берег и в бинокль смотрел, где лодочник. 2. Укажите предложение с обстоятельственным придаточным сравнения. 1) можно можно было видеть, как рдеют под солнцем гроздья рябины и боярки. 2) Левинсон, как ни крепко он спал, услышав свою фамилию, тотчас же открыл глаза и сел. 3) Федька видел, как с неудержимой силой на них из темноты летел высокий нос парохода, не замечая их, направляясь в самую середину судна. 4) Кустарник зашумел, будто рой пчел зажужжал над ветками. 3. Укажите предложение с обстоятельственным придаточным образа действия и сравнения. 1) Чаще стали слышны удары, будто гром катился раскатами. 2) Пётр завистливо крякнул, присматриваясь ко всему, что окружало его. 3) С мужем она обращалась так, как будто была старше и знала себя умнее его. 4) Незнакомец начал говорить, хотя своего имени и прошлого он еще не мог вспомнить. 4. Укажите предложение с обстоятельственным придаточным уступки. 1) Ока вздулась и потемнела от осеннего паводка, хотя по ней ещё шустро бегали последние катера. 2) Лишь только Иван Яковлевич уходит из дому, женский персонал приступает к готовке несложного обеда, мелкой стирке тут же на кухне, починке носильного белья и платья. 3) Вероятно, ни один спектакль не дал столько наслаждения жителю большого города, сколько дало островитянам зрелище этих разбитых, искалеченных кораблей. 4) Герасимов так глянул на своего подкормщика, что тот пожалел о заданном вопросе. 5. Укажите предложение с обстоятельственным придаточным степени и следствия. 1) Это была очень странная музыка, где каждый играл песнь своей родины, стараясь перекричать других. 2) Картина так дисгармонична, что от нее рябит в глазах. 3) Переменившийся ветер застилал пароход густым слоем дыма, так что трудно было дышать. 4) Ихтиандр часто пользуется этими течениями, когда ему нужно долго плыть вдоль берега. 6. Укажите предложение с обстоятельственным придаточным цели. 1) Я увидел на светлом пораненном смолистом кольце дерева какое-то темное пятно и вынул бинокль, чтобы рассмотреть подробней. 2) Очень скоро пришло от Кати новое письмо, настолько восторженное, что после него не встретиться с семьей Диабелли было бы просто невозможно. 3) Пётр Николаевич проснулся, когда сквозь дырявую сухую крышу начал пробиваться слабый свет. 4) Ихтиандр посмотрел на костюм таким взглядом, будто ему принесли змеиную кожу, и со вздохом начал одеваться. 7. Укажите предложение с обстоятельственным придаточным условия. 1) Чаще стали слышны удары, будто гром катился раскатами. 2) Ограда замка, так как это был настоящий замок, состояла из витых чугунных столбов, соединённых железным узором. 3) Если ты справишься с новыми обязанностями, я сделаю тебя постоянным слугой Ихтиандра. 4) Встретив неожиданно голубоглазую девушку в лавке продавца жемчуга Бальтазара, Ихтиандр так смутился, что выбежал из лавки и бросился к морю. 8. Укажите предложение с обстоятельственным придаточным причины. 1) Видно было, что никакие грустные мысли, никакие сомнения не омрачали Семена. 2) Насунув на голову шапку, я осторожно, чтобы не нарушить тишины этой хаты, открываю дверь. 3) Я рассеянно слушал его, терзаясь от собственных мыслей, когда в дальнем конце канавы послышался голос. 4) Ночь была темна, оттого что тучи покрывали небо и не пропускали света звёзд. 9. Укажите предложение с обстоятельственным придаточным времени. 1) Как только полк выехал из Озерного, пошёл холодный дождь. 2) Издали можно было видеть, как рдеют под солнцем гроздья рябины и боярки. 3) Гринюк, задрав подбородок, поглядел в небо, где время от времени выскальзывал из-под клочьев облаков почти правильный диск луны. 4) В ту минуту, когда Иван входил во двор, как раз наступила пауза. 10. Укажите предложение с обстоятельственным придаточным цели: 1) Цель моя состояла в том, чтобы побывать на Старой улице. 2) Старый паром вытащили на берег и крепко-накрепко привязали к древним могучим ветлам, чтобы его не унёс неудержимый весенний разлив. 3) Уткнув подбородок в снег, я мучительно соображал, что делать. 14) Едва он (Камушкин) сделал несколько шагов, как по верхушкам тростников сыпанула автоматная очередь.