Question

сколько решений имеет система уравнений
$\left \{ {{y=x^{3}=0 } \atop {x^{2}+y^{2}=4 }} \right.$ ?

Answer 1

Если у равен нулю, то х² = 4.

Отсюда система имеет 2 решения: х = 2 и х = -2.

Общее решение системы тоже имеет 2 решения.

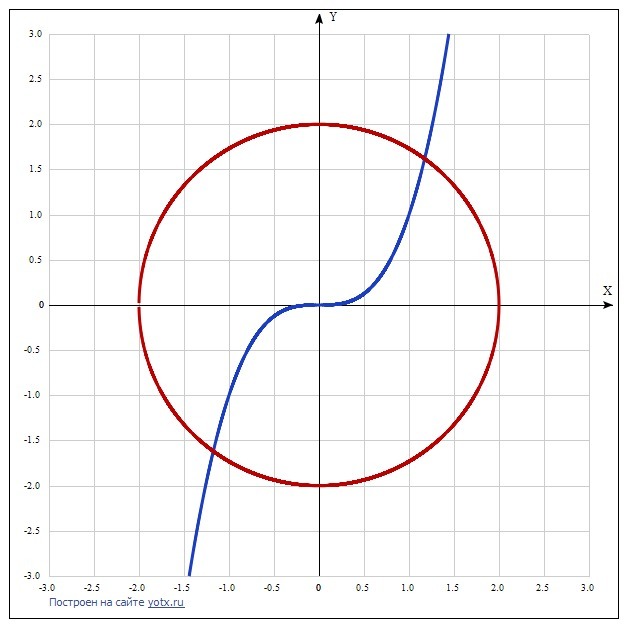
Графически данная система - это окружность радиуса 2 с центром в начале координат и кубическая парабола.

Они пересекаются в двух точках.

Для определения координат точек пересечения надо решить  систему уравнений:

{у = х³

{x² + y² = 4.

Подставим х³ во второе уравнение вместо у.

х² + х⁶ = 4.

Если заменить х² = t, то получим кубическое уравнение:

t³ + t - 4 = 0.

Для вычисления корней данного кубического уравнения используем формулы Кардано.

Решение даёт один вещественный корень: t = 1.3788.

Отсюда х = +-1,17422 и у = +-1,61901.