Предмет: Математика,
автор: matt911
Вычислить дифференциалы первого порядка от функции
Приложения:
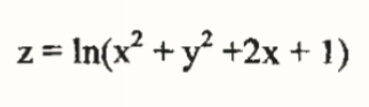
Ответы
Автор ответа:
0
Вычисляем частные производные функции :
По формуле выписываем дискриминант:
Похожие вопросы
Предмет: География,
автор: kittywoow
Предмет: Математика,
автор: Аноним
Предмет: Қазақ тiлi,
автор: nuradinkazyev
Предмет: Математика,
автор: Нигяр2005
Предмет: Музыка,
автор: ellosater1337