Предмет: Математика,
автор: nataliavolkova92
найти корни уравнения 1- ((3-2х)/(5-х))=(3/(3-х))-((х+3)/(х+1))
Приложения:
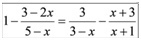
Ответы
Автор ответа:
1
Дробь равна 0, если числитель равен 0, а знаменатель нет.
{ -x^3-2x^2+2x^2+4x+3x+6-5x^2+x^3-15x+3x^2+30-6x = 0
{ x ≠ -1; x ≠ 3; x ≠ 5
Приводим подобные
{ -2x^2 - 14x + 36 = 0
{ x ≠ -1; x ≠ 3; x ≠ 5
Делим на -2
{ x^2 + 7x - 18 = 0
{ x ≠ -1; x ≠ 3; x ≠ 5
Решаем
{ (x + 9)(x - 2) = 0
{ x ≠ -1; x ≠ 3; x ≠ 5
Ответ: x1 = -9; x2 = 2
nataliavolkova92:
Огромное спасибо
Огромное пожалуйста
Похожие вопросы
Предмет: Русский язык,
автор: sonj020910
Предмет: Алгебра,
автор: Аноним
Предмет: Физика,
автор: egor8masterskikh
Предмет: Математика,
автор: molaev1973
Предмет: Геометрия,
автор: 50рублей