Question

Помогите разобраться с задачей.
Радиус окружности,описанной около треугольника равна 5. Может ли периметр этого треугольника быть равен 30?

Answer 1

пусть углы треугольника α ; β ;ω  , а стороны a ,b c  , тогда Р=2R·sinα+2R·sinβ+ 2R·sinω= 2R( sinα+sinβ +sinω) ≤ 10·3=30 , причем равенство достигается , если все синусы равны 1 , но это означает, что у треугольника 3 прямых угла , чего быть не может ⇒ периметр не может быть равен 30 ( всегда меньше при данных условиях)

Answer 2

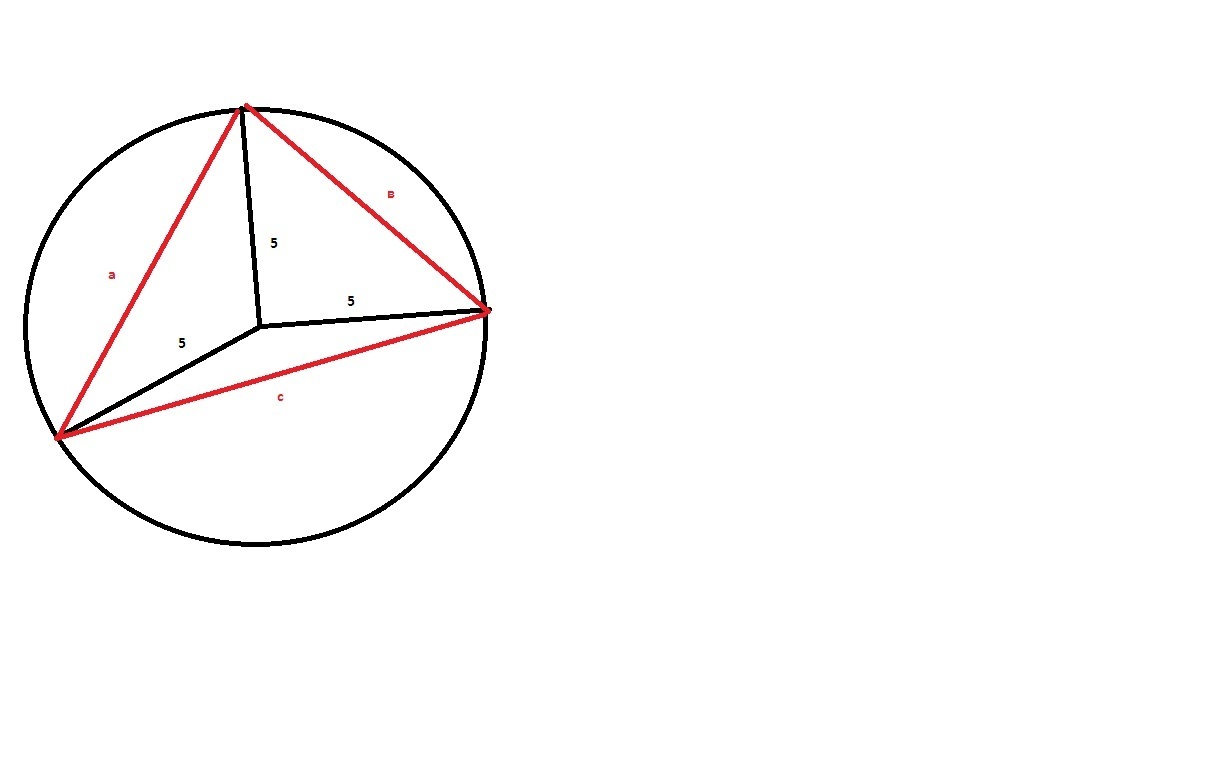
объясняю популярно и "на пальцах"   (смотри рисунок в файле)

по основному св-ву треугольника (треугольник может быть и тупоугольным, все равно получается так же) имеем

а<5+5

b<5+5

c<5+5

складываем , получаем

a+b+c<30, т.е периметр всегда меньше 30.