Question

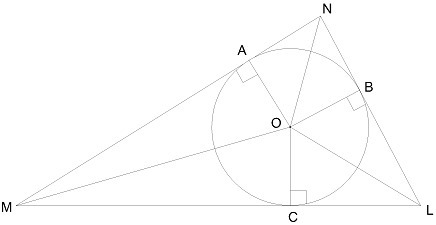
В треугольник вписана окружность. Вычисли неизвестные углы, если ∢OMN=28° и ∢ONL=31°.

Answer 1

Радиус перпендикулярен касательной в точке касания. Касательные из одной точки к окружности равны. Отрезки, соединяющие центр окружности и точку, из которой проведены касательные являются биссектрисами углов между этими касательными и углов между радиусами, проведенными к этим касательным в точки касания. Сумма острых углов прямоугольного треугольника равна 90°. Сумма всех углов с вершиной в центре окружности равна 360°.  Следовательно:

<NML=2*28=56°, <MNL=2*31=62°, <NLM=180-56-62=62°, <AOM=90-28=62°, <AON=90-31=59°, <NOB=<AON=59°, <MOC=<AOM=62°, <AOC=2*<AOM=124°, <AOB=2*<AON=118°, <COB=360-124-118=118°, <COL=<BOL=<COB:2 = 59°.