Предмет: Математика,
автор: serbinvova1337
Как решать такие примеры?
Приложения:
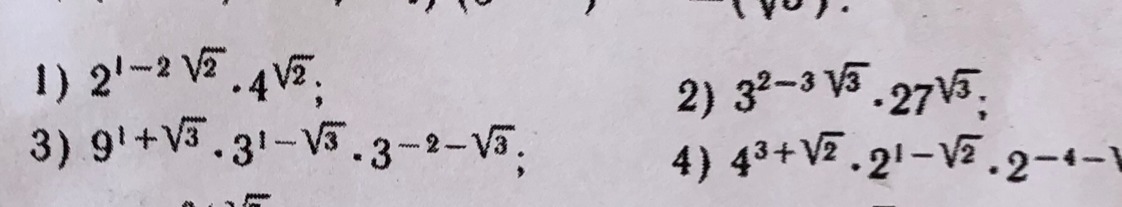
mmb1:
a^n*a^m=a^(m+n)
(a^m)^m=a^(m*n)
а цифрами?
вот и подставляйте вместо a m n цифры
какие именно?
какие в условии даны...
Ответы
Автор ответа:
1
а как тема по таким примерам называется? Решить то я решил, но откуда что берется вообще не понял.
формулы написала
Похожие вопросы
Предмет: История,
автор: yashinanani228
Предмет: Математика,
автор: 12341233234
Предмет: Английский язык,
автор: aishatop88
Предмет: Литература,
автор: farda6
Предмет: Математика,
автор: admolchanova