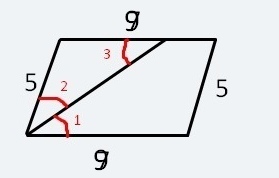
На отрезки какой длины делит сторону биссектриса одного из углов параллелограмма, если его периметр 28 см, а одна из сторон 5 см?
Ответы
Найдём величину каждой из сторон параллелограмма.
Т.к. одна из сторон равна 5 см, противоположная ей также равна 5 см. Вместе они составляют 10 см.
Две остальные стороны в сумме дают 28 - 10 = 18 см. Отдельно каждая = 18:2 = 9 см.
Угол 1 и угол 3 равны, т.к. они накрест лежащие.
Угол 1 и угол 2 равны, т.к. их образует биссектриса.
Благодаря тому, что угол 2 и угол 3 равны, образуется равнобедренный треугольник, в котором нам уже известна одна из сторон, которая равна 5 см. Т.к. треугольник равнобедренный, другая сторона, которая не биссектриса, также равна 5 см. Она же является частью ответа.
Чтобы найти второй отрезок, который образовала биссектриса, надо из длины основания вычесть длину уже известного отрезка: 9-5=4см.
Ответ: биссектриса делит основание на отрезки 5 см. и 4 см.