Предмет: Геометрия,
автор: odmenchan
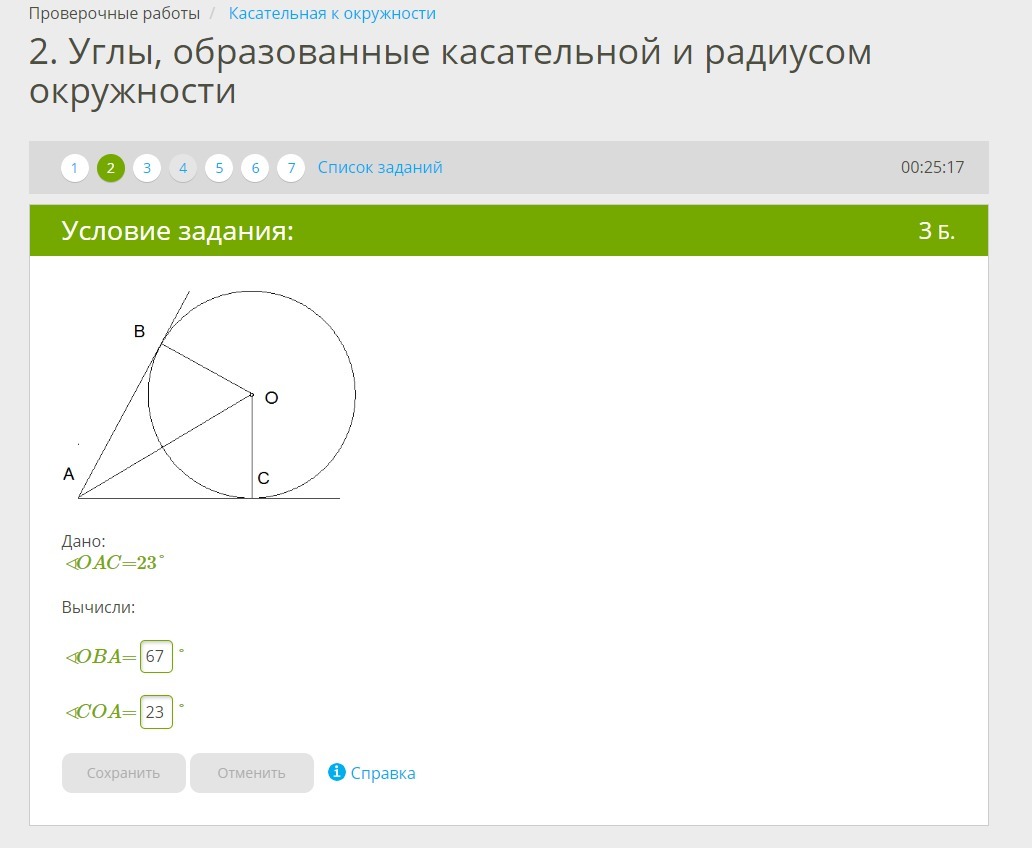
2. Углы, образованные касательной и радиусом окружности
Приложения:
Ответы
Автор ответа:
3
Радиус окружности перпендикулярен касательной в точке касания. Касательные из одной точки к окружности равны, а отрезок прямой, соединяющий эту точку и центр окружности, является биссектрисой углов между касательными и между радиусами, проведенными в точки касания. Таким образом, <OBA = 90°, <COA= 90-<OAC. <COA=90°-°23 = 67°.
Ответ: <OBA = 90°, <COF=67°.
Похожие вопросы
Предмет: Русский язык,
автор: artemmial737
Предмет: Английский язык,
автор: Donttakemymoney
Предмет: Литература,
автор: pelmeen20
Предмет: Математика,
автор: vonz