Предмет: Алгебра,
автор: Nastya171167
помогите решить уравнения
Приложения:
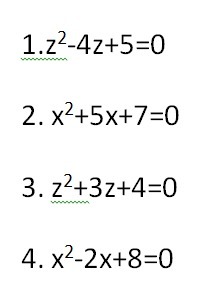
Ответы
Автор ответа:
6
Nastya171167:
спасибо огромное вы меня очень выручили у меня немного не получалось
не за что)
Автор ответа:
0
Воспользуемся формулой для корней квадратного уравнения, чтобы найти решения.
-b ± √b² - 4(ac)/2a
================================
Подставляем значения a = 1; b = -4 и c = 5 в формулу корней квадратного уравнения и решаем относительно z.
4±√( -4)² -4 *(1*5)/2*1
================================
Упростим
z = 2 ± i
2.
Воспользуемся формулой для корней квадратного уравнения, чтобы найти решения.
-b ± √b² - 4(ac)/2a
=========================
Подставляем значения a = 1; b = 5 и c = 7 в формулу корней квадратного уравнения и решаем относительно x.
-5 ± √5² - 4 * (1*7)/2*1
========================
Упростим
x = -5 ± i√3/2
3.
Воспользуемся формулой для корней квадратного уравнения, чтобы найти решения.
-b ± √b² - 4(ac)/2a
=======
Подставляем значения a = 1; b = 3; и c = 4 в формулу корней квадратного уравнения и решаем относительно z.
-3 ± √3² - 4*(1*4)/2*1
Упростим.
z = -3±i√7/2
4.
Воспользуемся формулой для корней квадратного уравнения, чтобы найти решения.
-b ±√b² -4(ac)/2a
Подставляем значения a = 1; b = -2 и c = 8 в формулу корней квадратного уравнения и решаем относительно x
2±(-2)²-4*(1*8)/2*1
Упростим
x = 1±i√7
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: viktoria5494
Предмет: Музыка,
автор: rebusivan854
Предмет: Обществознание,
автор: sofa119
Предмет: Математика,
автор: natasha9992