Предмет: Алгебра,
автор: redkina12
20 баллов!!Помогите пожалуйста
Приложения:
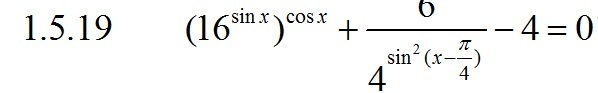
Ответы
Автор ответа:
1
Ответ.
redkina12:
спасибо большое) вы мой спаситель!!!
Похожие вопросы
Предмет: Алгебра,
автор: Vitpro2007
Предмет: Русский язык,
автор: q4a5z6sss
Предмет: Информатика,
автор: Justsofia2
Предмет: Математика,
автор: маль111