Предмет: Математика,
автор: pochtichudo
Найдите неопределённые интегралы . Результат проверить дифференцированием .
Приложения:
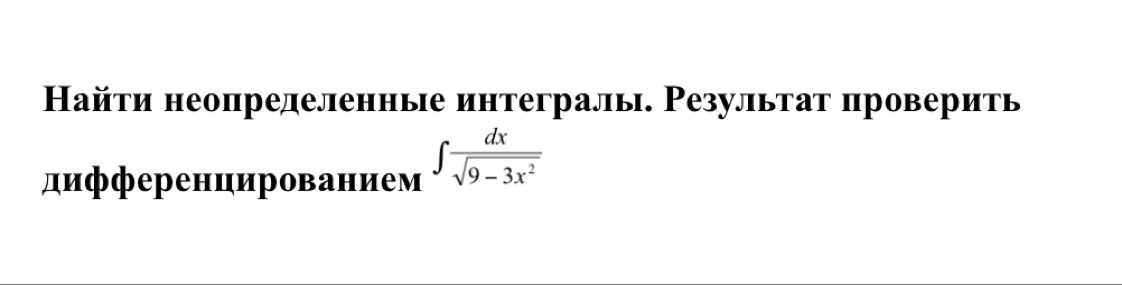
Аноним:
Мне лень делать проверку
Ответы
Автор ответа:
1
Найти неопределенный интеграл. Результат проверить дифференцированием.
Далее замена переменных
Сделаем обратную замену переменных
Следовательно
Проверка
Спасибо)
Похожие вопросы
Предмет: История,
автор: hakerhakerprokeller
Предмет: Математика,
автор: medcat0009000
Предмет: Немецкий язык,
автор: ivansidorov251286
Предмет: Математика,
автор: qazxcvbnm1
Предмет: Математика,
автор: Анастасия7833490