Предмет: Алгебра,
автор: Dima00002
Надо для вступительных экзаменов, распишите по подробнее, пожалуйста
Приложения:

oganesbagoyan:
{ |y| ≤ 8 ; |x|≤ 3. область прямоугольника с вершинами A( -3 ;-8) , B(-3;8) , C(3 ;8) и В(3 ; -8) . |3y-x(9 -x²)| ≥ 3 ⇔ |y -(1/3)*x(9 -x²)| ≥ 1
прямоугольник?
нет ,нужно добавить ограничение [ y ≤ (1/3) *x(9 -x²) - 1 ; y ≥ (1/3)x(9 -x²) *
даа, ничего я не знаю в математике:( , о каки вступительных может идти речь
плохо то,что я не могу использовать поле решения ( не знаю, что случилось )
ну так что?
теперь ответ можно написать?
Ответы
Автор ответа:
0
Это граничные линии. Берём точку "внутри" них - неравенство не выполнилось. Берём точку "вне" - неравенство выполнилось. Значит закрашиваем всё, что "вне" того участка
Строим , точно также берём пробную точку и закрашиваем всё внутри
С аналогично
Должно получиться как-то так
Приложения:
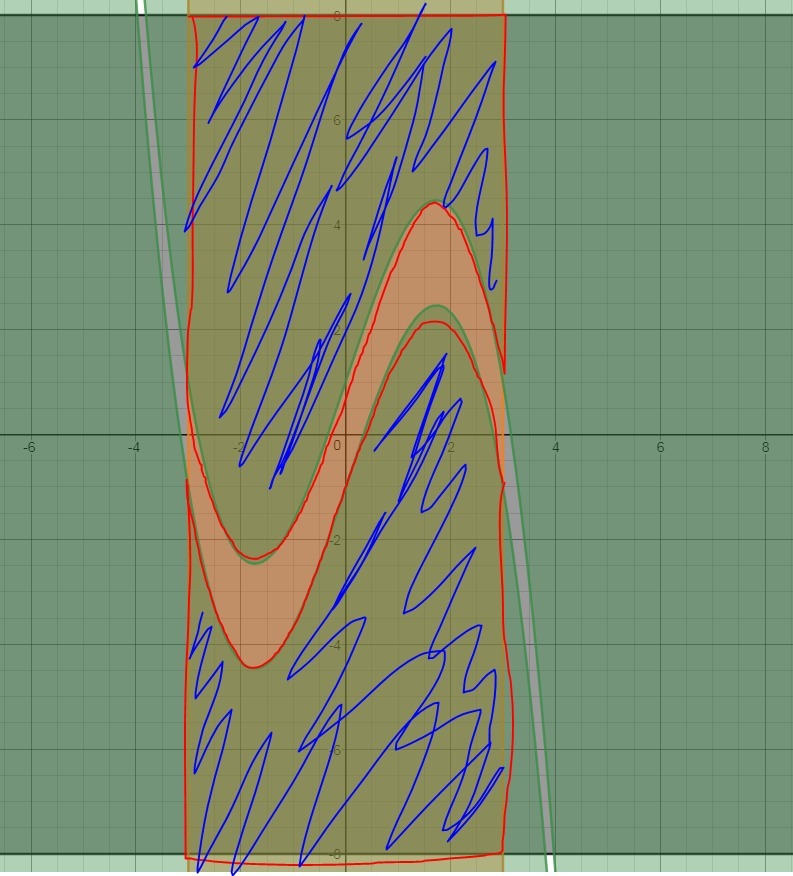
а ответ какой?
Похожие вопросы
Предмет: Геометрия,
автор: 0irinasmirnova0
Предмет: Русский язык,
автор: smwhle
Предмет: Физика,
автор: Торинид