Предмет: Алгебра,
автор: TequilaSunrise
помогите, пожалуйста ♡
Приложения:
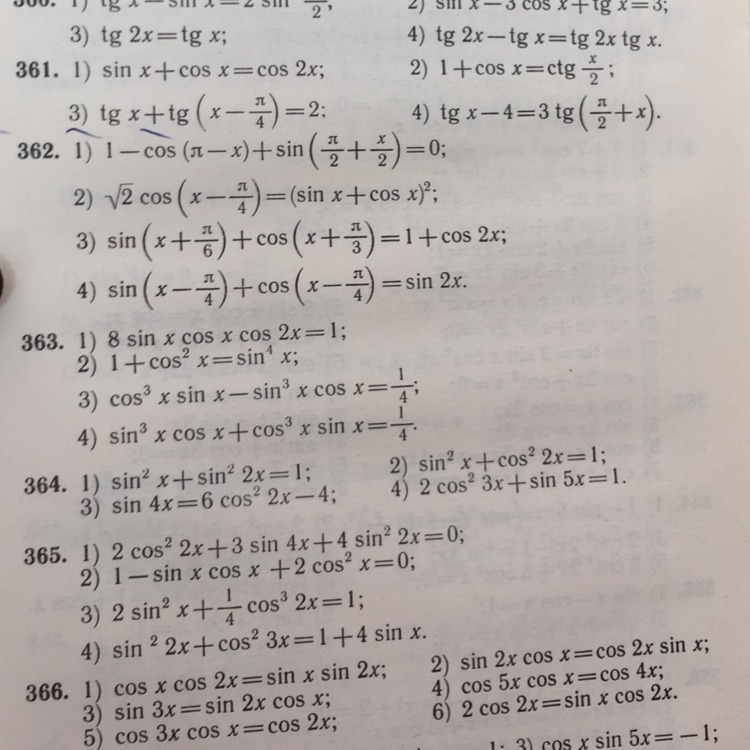
Ответы
Автор ответа:
2
Ответ.
Похожие вопросы
Предмет: Українська мова,
автор: hermionegranger771
Предмет: Информатика,
автор: jambulkarimov
Предмет: Русский язык,
автор: leyla1691
Предмет: Геометрия,
автор: чебуречик
Предмет: Математика,
автор: NoName999333