Предмет: Математика,
автор: NEON311

Решите уравнение.
Проблема с числителем
Аноним:
Ага
Ответы
Автор ответа:
3
это не уравнение у Вас, а неравенство
1^x +2^x< 3^(x+1)/(x+1)
1 +2^x< (3^(x+1))/(x+1)
построим графики
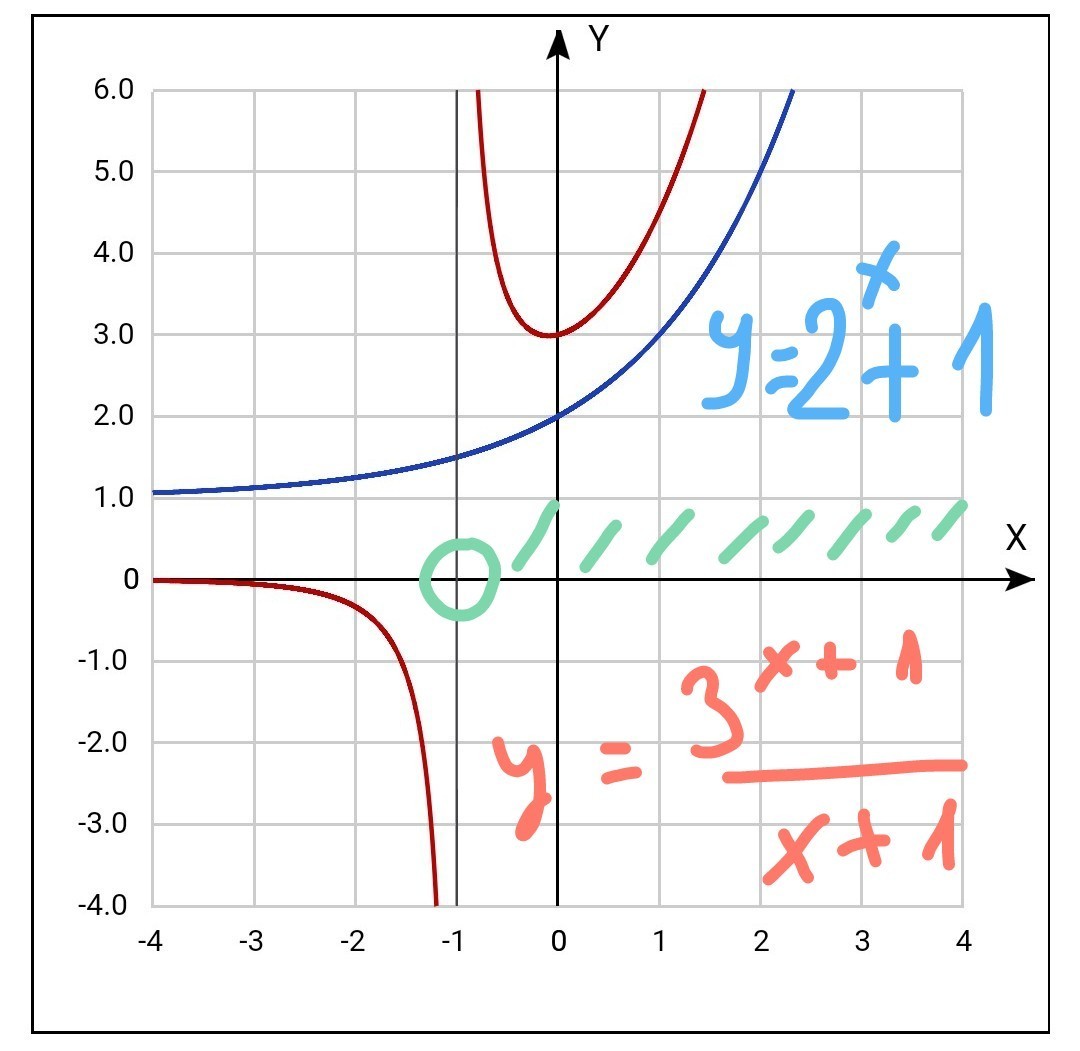
у1(х) = 1 + 2^x
у2(х) = (3^(x+1))/(x+1)
первый график y1(x) получается сдвигом графика 2^х на единицу вверх вдоль оси ординат
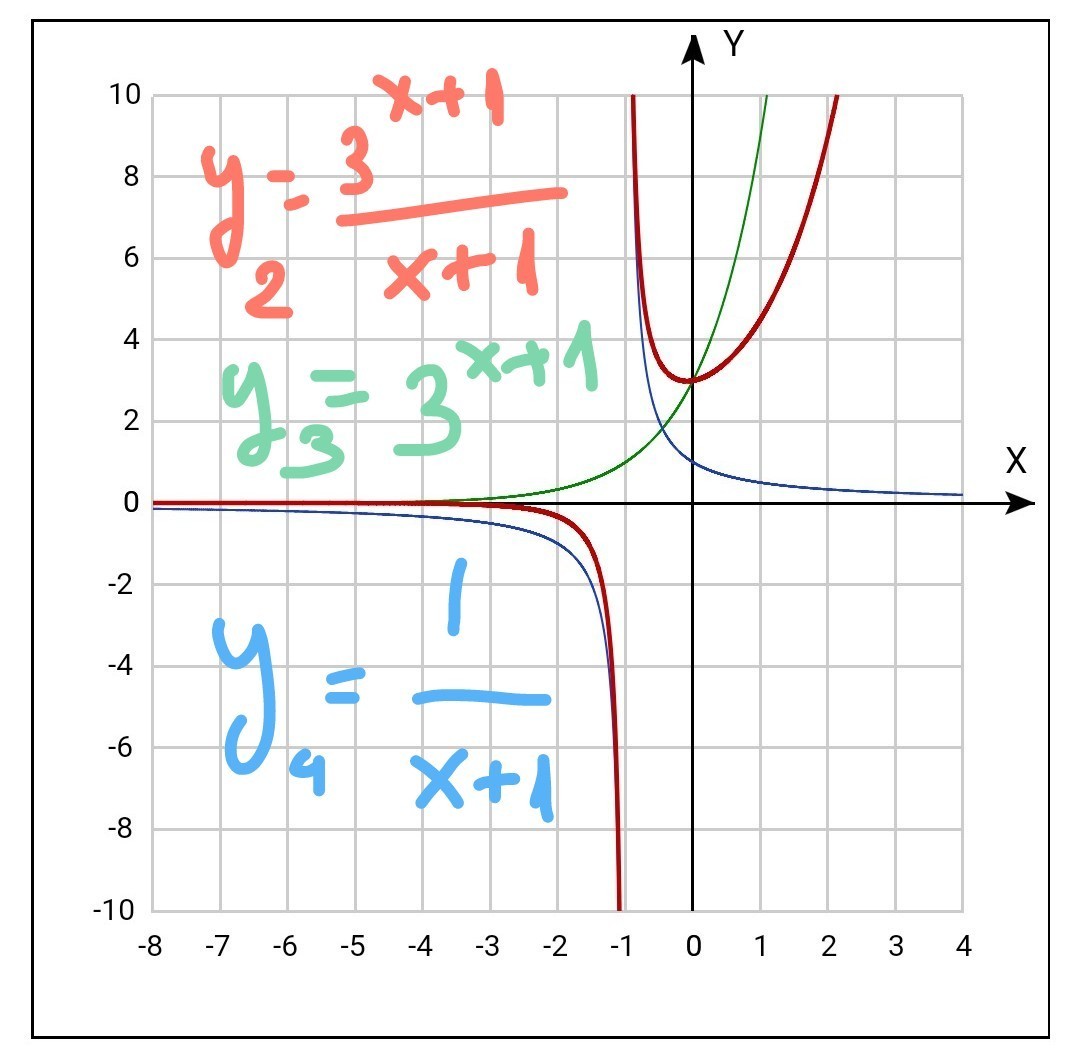
Вторая функция у2(х) является произведением двух функций
у2(х)=у3(х)•у4(х), где
у3(х)=3^(х+1) -
степенная функция,
строится переносом графика 3^х на 1 влево вдоль оси абсцисс
у4(х)=1/(х+1) -
гипербола, которая получается из гиперболы 1/х переносом её на 1 влево вдоль оси абсцисс.
Поэтому для построения
у2(х) поступаем так.
Берем точку (х*) , её ордината
у2(х*) находится как произведение ординат
у3(х*)•у4(х*)
у2(х*)=у3(х*)•у4(х*)
Свойства у2(х):
функция определена на
Dy2(x):х€(-∞, -1)v(-1,+∞)
область значений у2(х)
Ey2(x):y€(-∞,0)v(0,+∞)
ассимптоты для у2(х)
х=-1 и у=0
функция не является четной или нечетной, т.к.
у2(-х)=(3^(-x+1))/(-x+1))≠
≠у2(х)
у2(-х)≠-у2(х)
функция не является периодичной, т.к.
не существует T, такого что y2(x+T)=y2(x)
у2(х) не имеет нулей ,она не пересекает ОХ.
у2(х) пересекает
ось ОУ в точке
(0;у2(0))=(0;3)
у2(х)>0 при х>-1
у2(х)<0 при х<-1
найдем производную у2(х)
(см приложение)
функция убывает, когда у2'(х)<0
при
х€(-∞;-1)v(-1; ((1-ln3)/ln3) )
функция возрастает
при у2'(х)>0
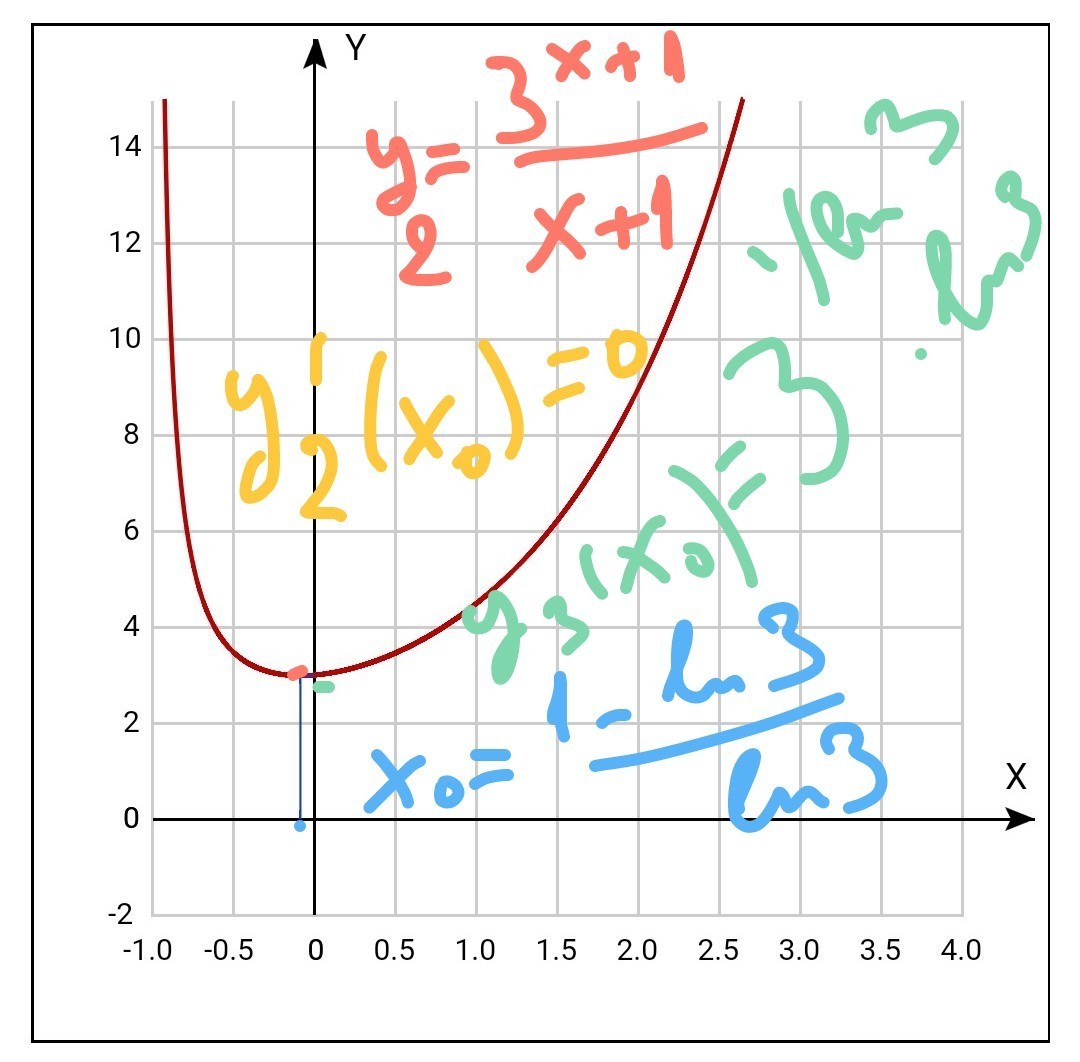
у2'(х°)=0=> х°=((1-ln3)/ln3)
(х°;у2(х°))- точка минимума у2(х)
(см рисунок)
график приведен на рисунке
Решением нашего неравенства
будет область, где у1 (х) будет находится под графиком у2(х) при одинаковых значениях х.
Нетрудно видеть,
что это будет при х> - 1
Ответ х> - 1
1^x +2^x< 3^(x+1)/(x+1)
1 +2^x< (3^(x+1))/(x+1)
построим графики
у1(х) = 1 + 2^x
у2(х) = (3^(x+1))/(x+1)
первый график y1(x) получается сдвигом графика 2^х на единицу вверх вдоль оси ординат
Вторая функция у2(х) является произведением двух функций
у2(х)=у3(х)•у4(х), где
у3(х)=3^(х+1) -
степенная функция,
строится переносом графика 3^х на 1 влево вдоль оси абсцисс
у4(х)=1/(х+1) -
гипербола, которая получается из гиперболы 1/х переносом её на 1 влево вдоль оси абсцисс.
Поэтому для построения
у2(х) поступаем так.
Берем точку (х*) , её ордината
у2(х*) находится как произведение ординат
у3(х*)•у4(х*)
у2(х*)=у3(х*)•у4(х*)
Свойства у2(х):
функция определена на
Dy2(x):х€(-∞, -1)v(-1,+∞)
область значений у2(х)
Ey2(x):y€(-∞,0)v(0,+∞)
ассимптоты для у2(х)
х=-1 и у=0
функция не является четной или нечетной, т.к.
у2(-х)=(3^(-x+1))/(-x+1))≠
≠у2(х)
у2(-х)≠-у2(х)
функция не является периодичной, т.к.
не существует T, такого что y2(x+T)=y2(x)
у2(х) не имеет нулей ,она не пересекает ОХ.
у2(х) пересекает
ось ОУ в точке
(0;у2(0))=(0;3)
у2(х)>0 при х>-1
у2(х)<0 при х<-1
найдем производную у2(х)
(см приложение)
функция убывает, когда у2'(х)<0
при
х€(-∞;-1)v(-1; ((1-ln3)/ln3) )
функция возрастает
при у2'(х)>0
у2'(х°)=0=> х°=((1-ln3)/ln3)
(х°;у2(х°))- точка минимума у2(х)
(см рисунок)
график приведен на рисунке
Решением нашего неравенства
будет область, где у1 (х) будет находится под графиком у2(х) при одинаковых значениях х.
Нетрудно видеть,
что это будет при х> - 1
Ответ х> - 1
Приложения:
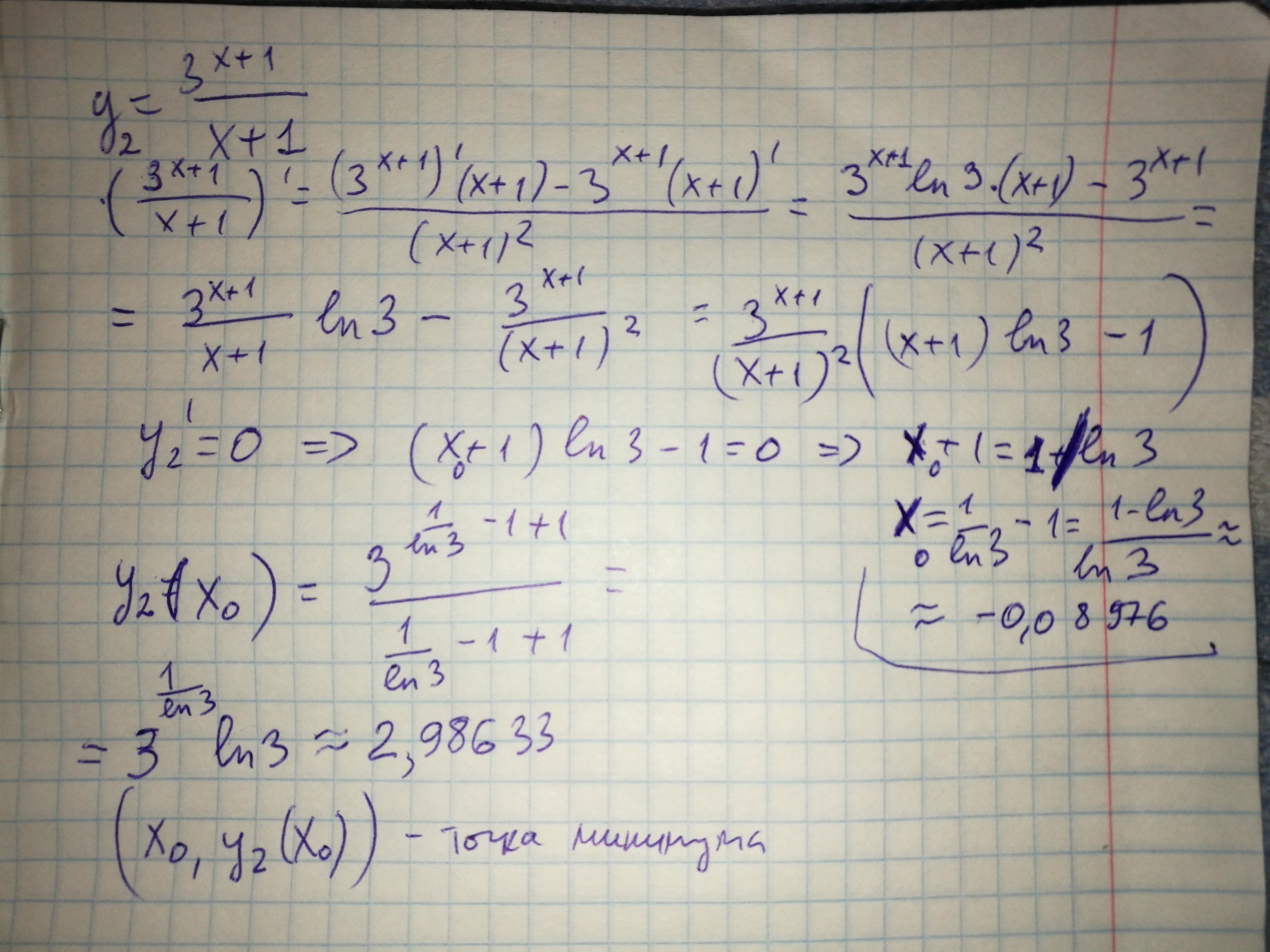
Вот еще: решение должно быть полным, знаете такое правило?
Самое убогое то что привели таблицу точек функции y = 2^x + 1
Здесь вообще возрастающая функция и y=2^x нужно поднять на 1 ед. вверх.
это задание решили вы, уважаемый ответчик, и мы будем обсуждать и критиковать его. и не важно кто и что умеет решать и у кого какой лучший друг планшет и что-то еще
цитирую "главное здесь- решение задачи" ГДЕ ЭТО РЕШЕНИЕ СОБСТВЕННО ГОВОРЯ? РЕШЕНИЕ, А НЕ КОПИЯ ГРАФИКА!
Ваааа
И сколько дней будет продолжаться ваш спор?
Повторюсь, вопросы не относящиеся к решению - удаляется комментарий с предупреждением
В смысле?
А, поняла
Похожие вопросы
Предмет: Английский язык,
автор: nazar3340215
Предмет: Другие предметы,
автор: kometamiloty
Предмет: Химия,
автор: Milana8414
Предмет: Химия,
автор: Кираз
Предмет: Обществознание,
автор: критина890