Предмет: Алгебра,
автор: kastahoff
довести тождество sinα+sinβ+sin(α-β)=4 sin/2*cos/2*cos α-β/2
Приложения:
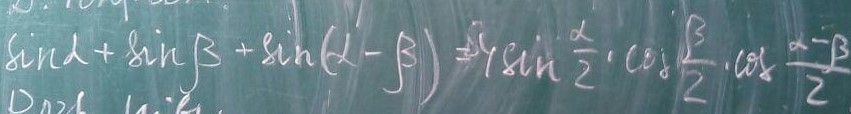
Ответы
Автор ответа:
8
Автор ответа:
1
sina+sinb+sin(a-b)=4*sina/2*cosb/2*cos(a-b)/2
sina+(sinb+sin(a-b))=2*sina/2*cosa/2+
2sin(b+a-b)/2*cos(b-a+b)/2=
2sina/2*(cosa/2+cos(b-a/2)=
2*sina/2*(2*cos(a/2+b-a/2)/2*cos(a/2-b+a/2)/2)
=4*sina/2*cosa/2*cos(a-b)/2
sina+(sinb+sin(a-b))=2*sina/2*cosa/2+
2sin(b+a-b)/2*cos(b-a+b)/2=
2sina/2*(cosa/2+cos(b-a/2)=
2*sina/2*(2*cos(a/2+b-a/2)/2*cos(a/2-b+a/2)/2)
=4*sina/2*cosa/2*cos(a-b)/2
Похожие вопросы
Предмет: Математика,
автор: soldy21
Предмет: Математика,
автор: nikitinavika597
Предмет: Математика,
автор: kasimbekovafarangiz
Предмет: Литература,
автор: bredikhina1977
Предмет: Математика,
автор: vanek20042016