Помогите решить уравнения
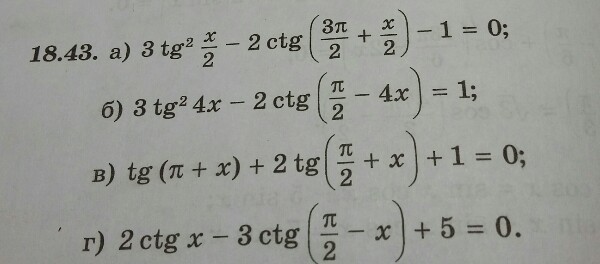
Ответы

task/29537604 Решить уравнения 18.43.
Используем формулы приведения , получаются квадратные уравнения относительно тригонометрических функции
a) 3tg²(x/2) - 2ctg(3π/2 + x/2) - 1 = 0 ⇔3tg²(x/2) + 2tg(x/2) - 1 = 0 ⇔
[ tg(x/2) = - 1 ; tg(x/2) = 1/3 .⇔[ x/2 = - π/4 +πn ; x/2 = arctg(1/3) + πn ,n ∈ ℤ.⇔
[ x = - π/2 +2πn ; x = 2arctg(1/3) + 2πn , n ∈ ℤ.
б) 3tg²4x - 2ctg(π/2 - 4x) = 1 ⇔3tg²4x -2tg4x - 1 =0 ⇔[ tg4x =1 ; tg4x = -1/3.⇔
[ 4x =π/4 +πn ; 4x = -arctg(1/3)+πn ,n ∈ ℤ. ⇔
[ x =π/16 +(π/4)n ; x = - (1/4)arctg(1/3)+(π/4)n ,n ∈ ℤ.
в) tg(π +x) +2tg(π/2+x) +1 = 0 ⇔ tgx - 2ctgx +1 = 0⇔ tg²x +tgx - 2 =0 ⇔
⇔[ tgx =1 ; tgx = -2.⇔ [ x =π/4 +πn ; x = -arctg2 +πn ,n ∈ ℤ.
г) 2ctgx -3ctg(π/2 - x) +5 = 0 ⇔ 2ctgx -3tgx + 5 =0⇔ 2ctg²x +5ctgx -3 =0 ⇔
квадр. уравнение относ. ctgx: D = 5²- 4*2*(-3) = 49 =7²; ctgx =( -5 ± 7)/2*2
[ ctgx = - 3 ; ctgx = 1/2. ⇔ [ x = - arcctg3 +πn ; x = arcctg(1/2) +πn ,n ∈ ℤ.