Question

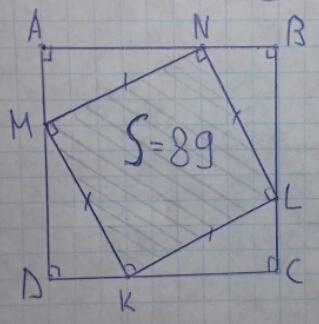
Внутри большего квадрата расположен меньший квадрат площади 89. Известно, что длины отрезков, на которые сторона большего квадрата делится вершинами меньшего квадрата, — натуральные числа. Чему равна площадь большего квадрата?

Answer 1

A, B, C и D - вершины большого квадрата; M, N, L и K - вершины маленького квадрата, при этом M∈DA, N∈AB, L∈BC, K∈CD.

Пусть ∠ANM = α, тогда ∠AMN = 180°-90°-α = 90°-α.

∠AMD - развёрнутый, значит ∠DMK = 180°-∠AMN-90° = 90°-90°+α = α.

∠DKM = 90°-α.

ΔANM = ΔDMK по трём углам, поэтому DM=AN ⇒ AM+AN=AD - сторона большого квадрата.

Площадь маленького квадрата 89, значит квадрат его стороны равен 89 (MN²=89). ΔANM - прямоугольный, поэтому по теореме Пифагора:

AM²+AN²=MN²=89.

AM² и AN² это квадраты натуральных чисел. Для суммы 89 подходят только квадраты чисел 5 и 8.

AM+AN = 5+8 = 13 = AD

$\tt \displaystyle S_{ABCD} =AD^2 =13^2 =169$

Ответ: 169.