Предмет: Алгебра,
автор: HNLLZ
Ребят, помогите, пожалуйста, успросить выражение.
Должно быть 2 способа, первый когда а>b, второй а
Приложения:
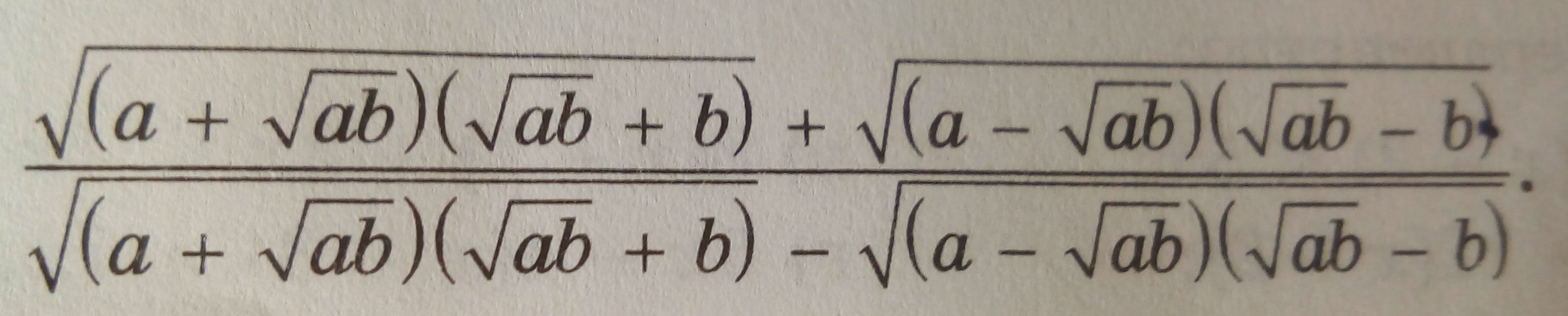
HNLLZ:
Второй а
а меньше б
То есть решение с модулями обязательно
Решите на листочке, пожалуйста
is answer a/b?
No
*упростить (опечатка в задании)
Да вроде не трудно
Сейчас, перепишу более-менее разборчивым почерком
Ответы
Автор ответа:
2
Идея решение проста: домножать дробь на сопряженное выражение знаменателя. 2 случая появляются после того, как из-под корня вылазит модуль. Решение на фото.
Приложения:

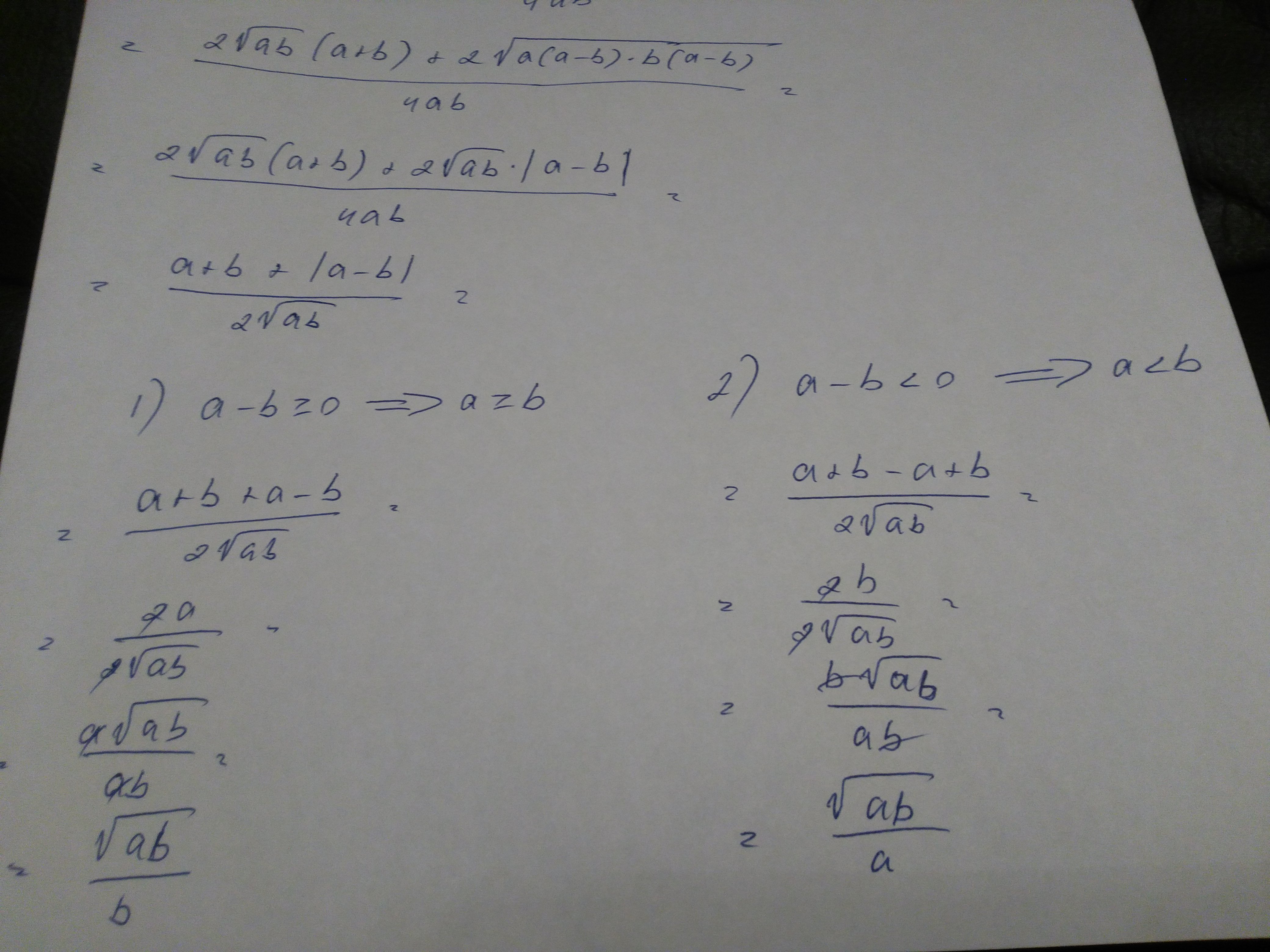
А в числителе квадрат суммы
Не понимаю, почему числитель возвели в квадрат, а знаменатель нет, и там просто так корни убрали
Ой
Глупость спросила какую-то
Я поняла теперь
Еще один момент в конце решения.. Почему а≥b? Просто в ответе а строго больше b
Я знаю, что модуль открывается с ≥, то есть по идее правильно у Вас. В учебнике отпечатка, получается?
Можно и так и так, потому что при a=b, |a-b|=|0|=0 и от знака, с которым раскрываем модуль, ничего не зависитэ
Так что и тут и там правильно
Оо, спасибо, теперь все понятно! Реально выручили, добра Вам;)
Похожие вопросы
Предмет: Физика,
автор: nikdissv
Предмет: Русский язык,
автор: dina0109
Предмет: Физкультура и спорт,
автор: rejepalyyewa
Предмет: Литература,
автор: ovanesyantatyana
Предмет: Алгебра,
автор: xabizat14