Question

a)Решите тригонометрическое уравнение
$2cos^3x=sin(\frac{\pi }{2}-x)$
б)Найдите все корни этого уравнения, принадлежащие отрезку [$-4\pi$;$-\frac{5\pi }{2}$]

Answer 1

Используем формулы приведения и формулу двойного угла:

а)

$2\cos^3x=\sin\left(\dfrac{\pi}{2}-x\right) \medskip \\ 2\cos^3x=\cos x \medskip \\ 2\cos^3x-\cos x=0 \medskip \\ \cos x\left(2\cos^2x-1\right)=0 \medskip \\ \cos x\cdot \cos 2x=0 \medskip \\ 1)\cos x = 0 \medskip \\ x=\dfrac{\pi}{2}+\pi k, k\in \mathbb{Z} \medskip \\ 2) \cos 2x=0 \medskip \\ 2x=\dfrac{\pi}{2}+\pi m, m\in \mathbb{Z} \medskip \\ x=\dfrac{\pi}{4}+\dfrac{\pi m}{2}, m\in \mathbb{Z}$

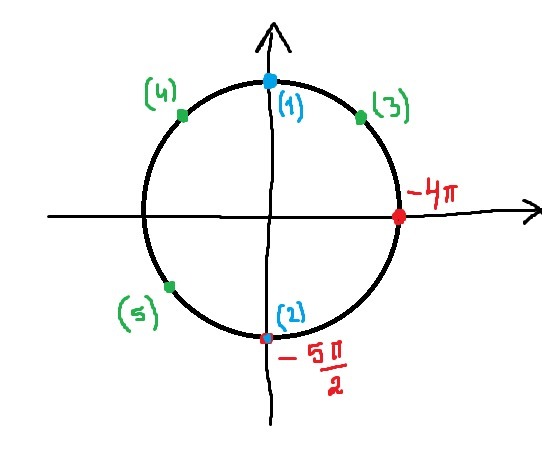
Выборку произведем на окружности:

б) Синие точки - первая серия корней, зеленые - вторая, красные - данный отрезок

Найдем угловую меру синих и зеленых точек

$(1) -4\pi +\dfrac{\pi}{2}= \dfrac{\pi-8\pi}{2}=-\dfrac{7\pi}{2} \medskip \\ (2) -\dfrac{7\pi}{2}+\pi=\dfrac{2\pi - 7\pi}{2}=-\dfrac{5\pi}{2} \medskip \\ (3)-4\pi + \dfrac{\pi}{4}=\dfrac{\pi-16\pi}{4}=-\dfrac{15\pi}{4} \medskip \\ (4)-\dfrac{15\pi}{4}+\dfrac{\pi}{2}=\dfrac{2\pi-15\pi}{4}=-\dfrac{13\pi}{4} \medskip \\ (5) -\dfrac{13\pi}{4} + \dfrac{\pi}{2}=\dfrac{2\pi-13\pi}{4}=-\dfrac{11\pi}{4}$