Предмет: Алгебра,
автор: mirna83
Чи є послідовність арифметичною прогресією?
Приложения:
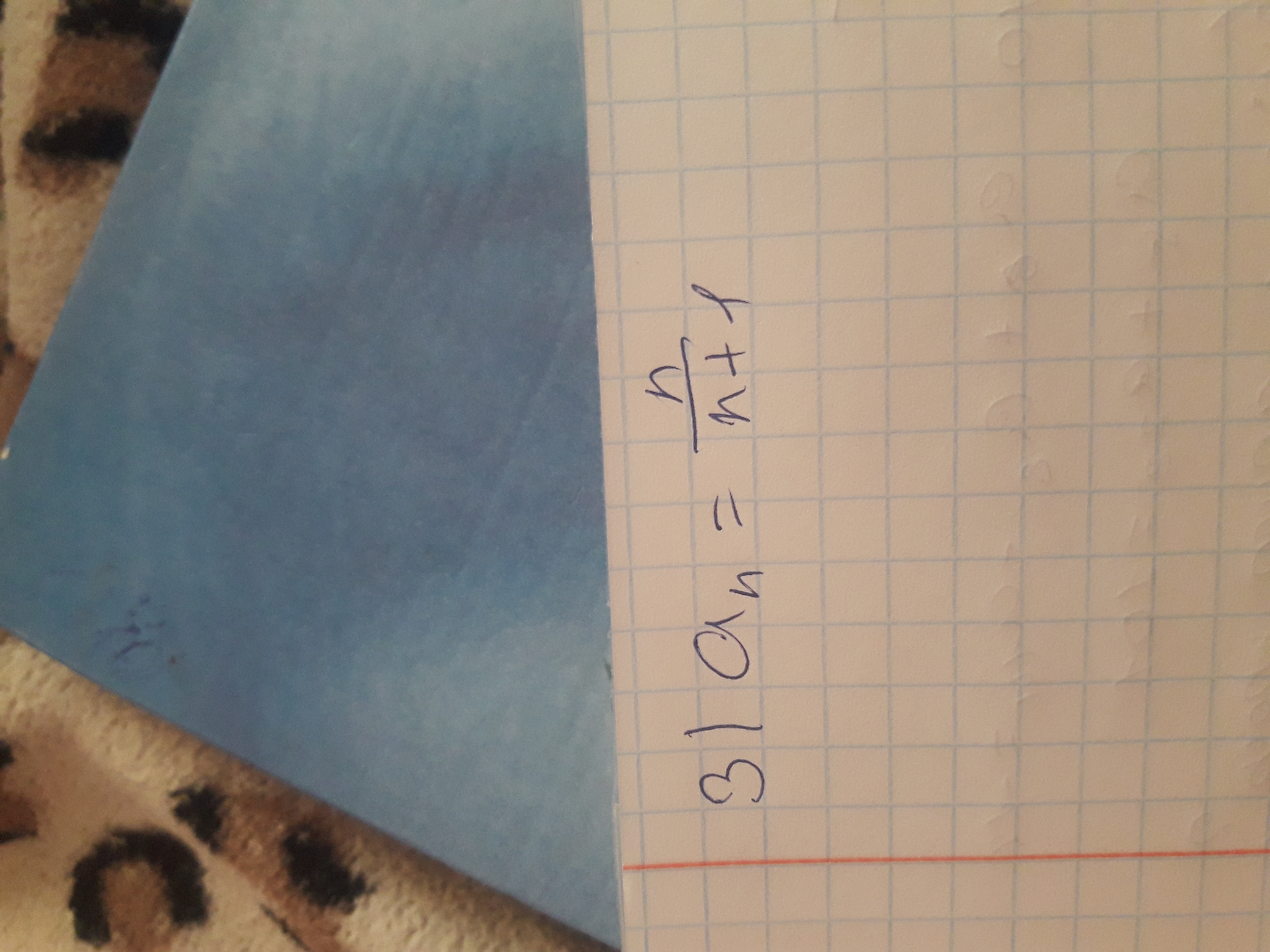
Ответы
Автор ответа:
2
....................................................................
Ответ: данная последовательность НЕ является арифметической прогрессией.
Похожие вопросы
Предмет: Алгебра,
автор: pupil216
Предмет: Қазақ тiлi,
автор: uruzgalivaruzan
Предмет: Русский язык,
автор: ramazanalmuhamed26
Предмет: Физика,
автор: Osendo