Предмет: Алгебра,
автор: holmskaja
Помогите разобраться с решением логарифмов
Приложения:
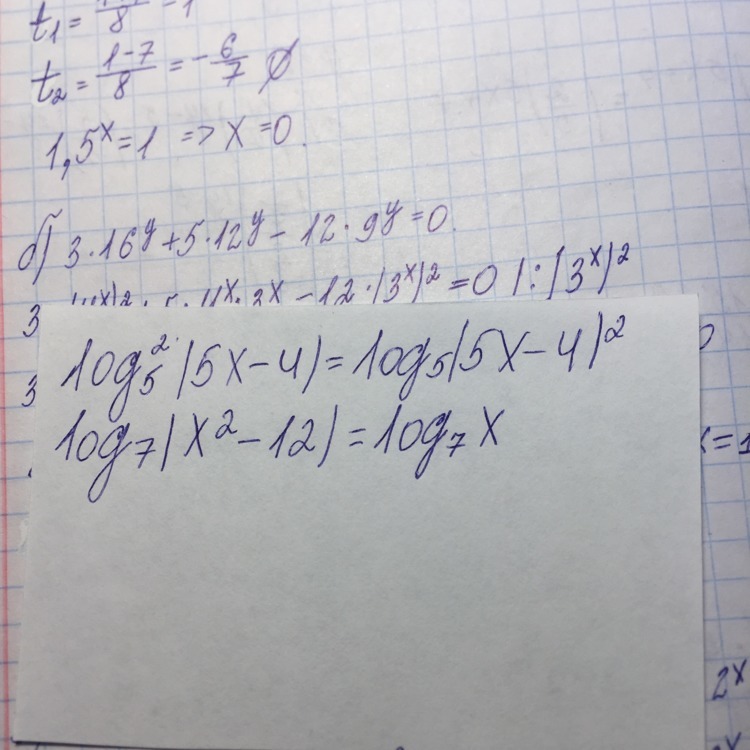
Ответы
Автор ответа:
1
Ответ: 1; 29/5.
ОДЗ:
х > 0
х^2 - 12 > 0
Корень х = -3 не удовл.ОДЗ => не является корнем уравнения.
Ответ: 4.
holmskaja:
Спасибо большое)
Поможете с другими логарифмами в профиле?)
Похожие вопросы
Предмет: Математика,
автор: bakinanatalia79
Предмет: Математика,
автор: jsjsjsjss45
Предмет: История,
автор: mamadzanovmmm6953
Предмет: Физика,
автор: supernickitru
Предмет: Алгебра,
автор: DilnazRakhimova