Предмет: Алгебра,
автор: ЭрикаСыпко
Доказать методом математической индукции. Срочно, пожалуйста!
Приложения:
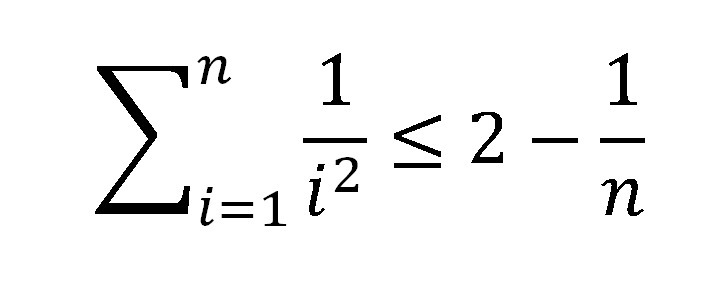
Ответы
Автор ответа:
1
1. База индукции: n = 2.

Верно.
2. Пусть n = k. Предположим, что для этого n неравенство выполняется.
3. Пусть n = k + 1. Тогда

Отсюда следует, что неравенство справедливо для всех натуральных k, а значит, и для всех натуральных n (пункт 2).
Верно.
2. Пусть n = k. Предположим, что для этого n неравенство выполняется.
3. Пусть n = k + 1. Тогда
Отсюда следует, что неравенство справедливо для всех натуральных k, а значит, и для всех натуральных n (пункт 2).
Похожие вопросы
Предмет: Литература,
автор: 6ghost6light6
Предмет: Литература,
автор: luba789p47m9p
Предмет: Математика,
автор: kegiazaryan81
Предмет: Химия,
автор: sifrel98
Предмет: Математика,
автор: Аноним