Предмет: Алгебра,
автор: holmskaja
Показательное уравнение
Приложения:
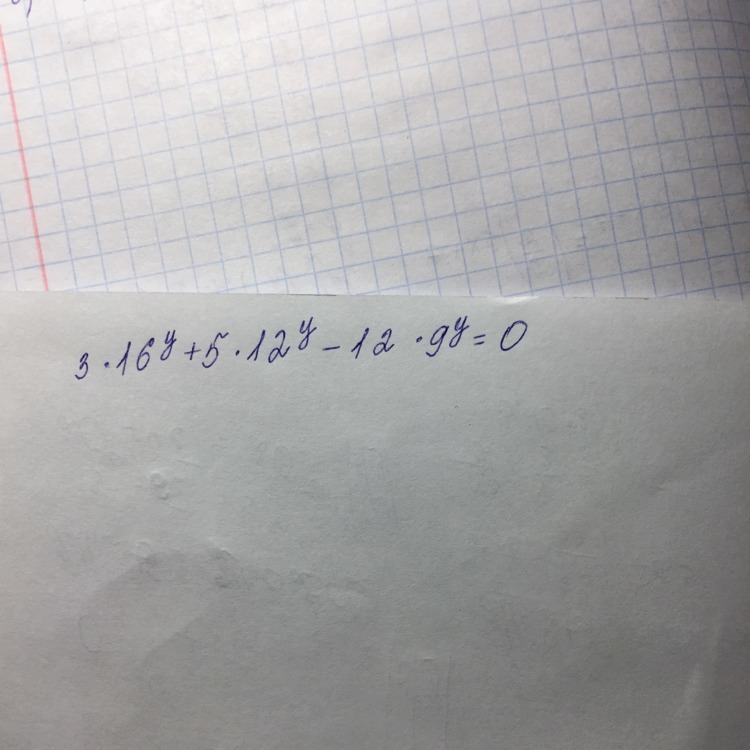
Ответы
Автор ответа:
1
Вместо у напишу х (для удобства записи выражений)
3·16ˣ + 5·12ˣ - 12·9ˣ = 0;
3·(4ˣ)² + 5·4ˣ · 3ˣ - 12·(3ˣ)² = 0|:(3ˣ)²;
3·((4/3)ˣ)² + 5·(4/3)ˣ - 12 = 0; - квадратное уравнение относительно (4/3)ˣ.
D = 25 + 144 = 169; √D = 13;
(4/3)ˣ = (-5 + 13)/6 = 8/6 = 4/3; х = 1.
(4/3)ˣ = (-5 - 13)/6 = -3 - не имеет решений
Ответ: 1.
ruslank1460:
Это уравнение надо решить?
Да,спасибо большое )))
Автор ответа:
0
Разделим обе части уравнения на
; t > 0
Ответ: у = 1
Похожие вопросы
Предмет: Информатика,
автор: valmierosupp
Предмет: Французский язык,
автор: aydi5577
Предмет: Физика,
автор: crazy4470
Предмет: Биология,
автор: али171
Предмет: История,
автор: cuteferrret