Предмет: Алгебра,
автор: miralina11
ПОЖАЛУЙСТА ПОМОГИТЕ! найдите увеличенную в 20 раз сумму корней
Приложения:
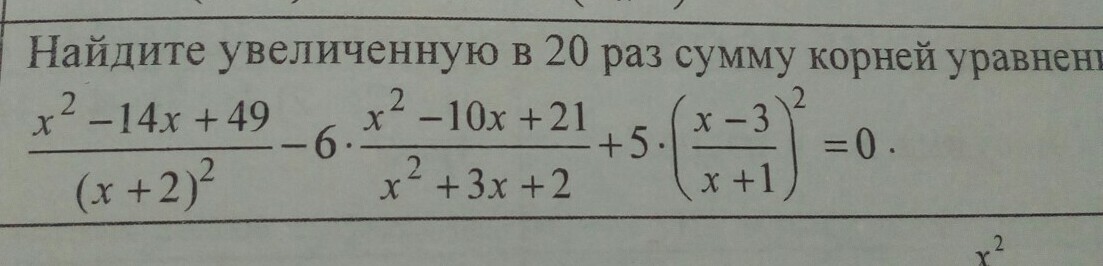
Ответы
Автор ответа:
1
Разложим все выражения на множители:
Пусть
или
Сумма корней равна -0.25 + (-0.2) = -0.45. -0.45 * 20 = 9
Ответ: 9
miralina11:
спасибо, можешь еще одно решить?
почему а =5б
У нас получилось уравнение (a-b)(a-5b)=0. Отсюда либо a-b=0, либо a-5b=0. Переносим члены с b в другую сторону: a=b или a=5b.
Похожие вопросы
Предмет: Биология,
автор: shukurovam87
Предмет: Українська мова,
автор: ivasukulia08
Предмет: Алгебра,
автор: zemgrief098
Предмет: Математика,
автор: liliya251974
Предмет: Математика,
автор: grigoryankaren78