Предмет: Алгебра,
автор: ilona75
помогите пожалуйста очень срочно!!!! . Нужно решить методом замены , заранее огромное спасибо
Приложения:
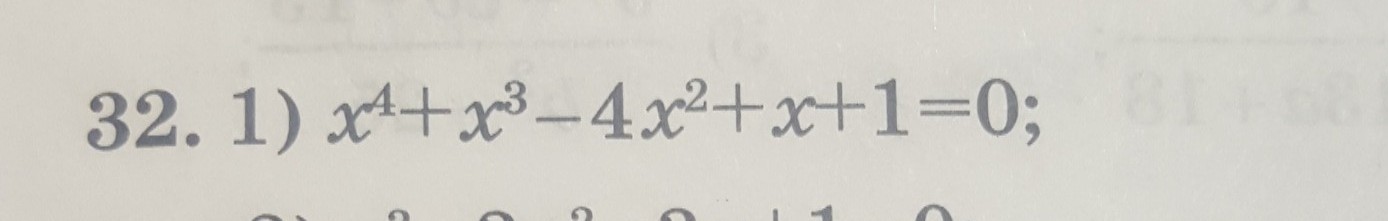
Аноним:
(x^2+1)/x = t
А можно пожалуйста после этого решение вместе с ответом
меня смущает условие: именно заменой) а другой вариант возможен...? очевидный корень х=1, можно разделить уголком...
Другой вариант возможен но нам задали заменой
Пожалуста можете дать мне все решение
Ответы
Автор ответа:
5
Разделим левую и правую части уравнения на х², получим
Сделаем следующую замену. Пусть , тогда получим квадратное уравнение относительно t
По т. Виета:
Обратная замена
Похожие вопросы
Предмет: Русский язык,
автор: gulya7465
Предмет: Математика,
автор: versachexdior
Предмет: Русский язык,
автор: Mishigan
Предмет: Математика,
автор: anya0817
Предмет: Математика,
автор: маша1175