Предмет: Математика,
автор: CorpseYT
В школе проболел на этой теме и позавчера на паре плохо понял. Как такое решать? Завтра проверочная будет. Помогите :c
Приложения:
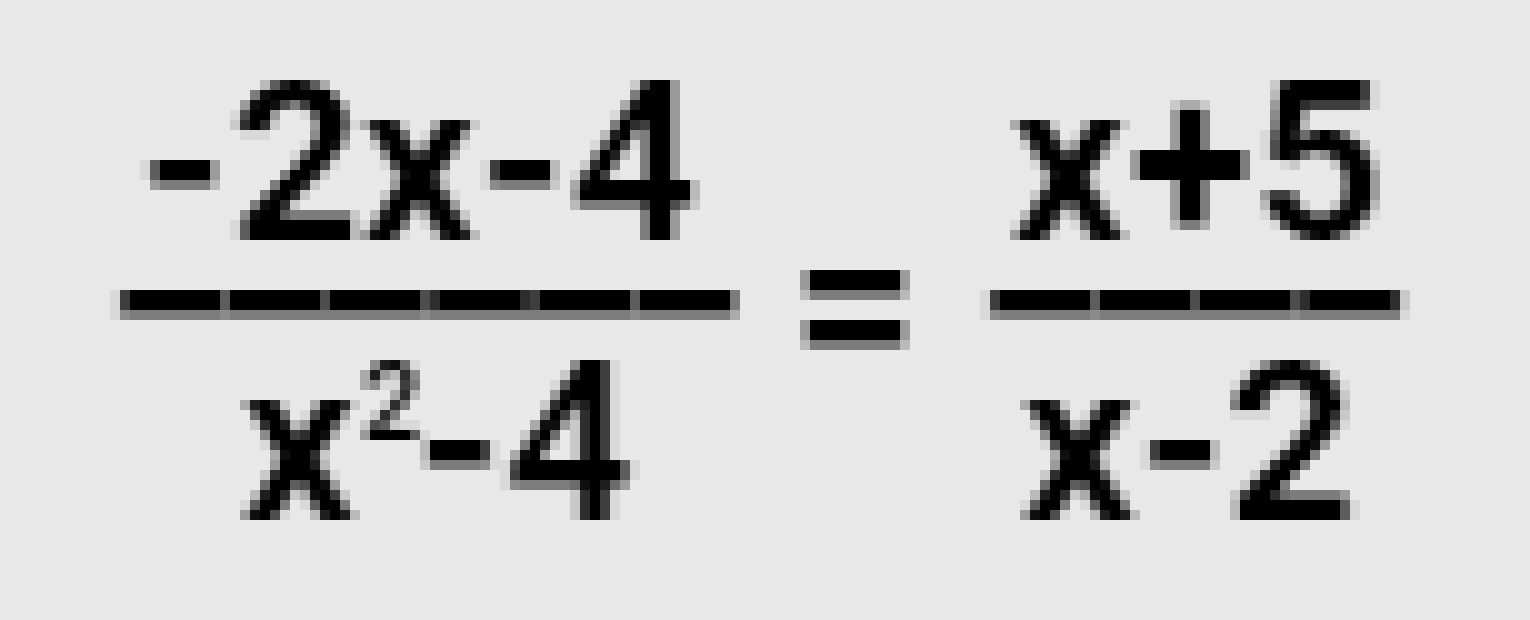
Ответы
Автор ответа:
0
Такие уравнения решаются приведением к общему знаменателю. Важно не забыть про область допустимых значений и исключить те корни, которые не подходят.
ОДЗ: x не равен 2 или -2.
Левая часть равна нулю тогда, когда хотя бы один из множителей числителя равен нулю. (x+2) не может быть равен нулю, поэтому равен нулю (x+7). Значит, x = -7.
Ответ: -7
CorpseYT:
Как вычислить это ОДЗ?
В ОДЗ указываются все возможные значения x. На ноль делить нельзя, поэтому исключаются все случаи, когда в знаменателе получается 0. Если решить уравнение x^2 - 4 = 0 для левого знаменателя, получатся корни 2 и -2.
Похожие вопросы
Предмет: Геометрия,
автор: cujkevictamila
Предмет: Алгебра,
автор: Vadisan
Предмет: Геометрия,
автор: maxmudovtural06
Предмет: Математика,
автор: Умник17111