Помогите пожалуйста.
Найти область изменения функций(E(f))
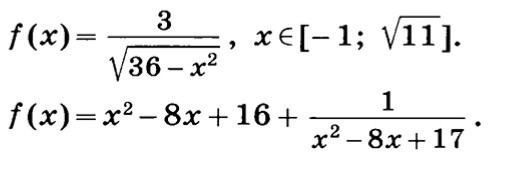
Ответы
1)
ОДЗ : 36 - x² > 0; (6 - x)(6 + x) > 0
Метод интервалов : x₁ = -6; x₂ = 6
------------ (-6) +++++++++++ (6) -------------> x
ОДЗ : x ∈ (-6; 6)
Заданный в условии интервал [-1; √11] ⊂ (-6; 6) - входит в ОДЗ.
В знаменателе под корнем стоит квадратичная функция y=36-x², графиком которой является парабола с ветками, направленными вниз. Значит, наибольшее значение функция y=36-x² принимает в точке вершины
x₀ = -b/2a = -0/(-2)=0; x₀ ∈ [-1; √11]
У дроби чем больше знаменатель, тем меньше ее значение. Значит, в точке x₀=0 функция f(x) будет иметь наименьшее значение. Осталось найти значение функции в точке x₀ = 0 и проверить границы интервала [-1; √11]
E(f) = [0,5; 0,6], x∈[-1; √11]
=================================================
2)
В знаменателе дроби - сумма двух положительных чисел всегда больше нуля. Дробь будет иметь наибольшее значение, когда в знаменателе наименьшее значение.
При x=4 ⇒ - наибольшее значение дроби
График функции y = (x - 4)² - парабола, ветви направлены вверх. Минимальное значение принимает в точке вершины x₀ = 4. Сверху не ограничена.
E(f) = [1; +∞)