Question

Помогите построить график функции (мне достаточно знать точки и как их получили) $y = |x^{2} - |x| - 2|$

Answer 1

1. Строим сначала график функции y = x² - x - 2. Графиком квадратичной функции является парабола, ветви направлены вверх

x = -b/2a = 1/2

y(1/2) = 1/4 - 1/2 - 2 = -2.25

Получим точку вершины параболы: (0.5; -2.25).

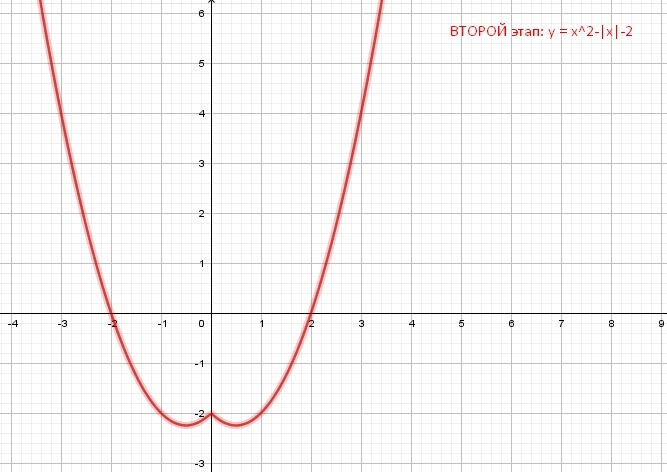
2. График функции y = x² -x - 2 симметрично отобразим относительно оси ординат, в результате получим график функции y = x² - |x| - 2

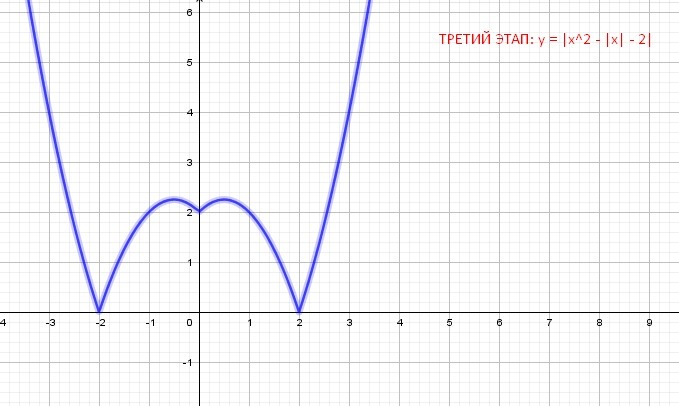
3. Нижнюю часть графика функции y = x² - |x| - 2 отобразим в положительную полуоси ординат, получим график функции y=|x^2-|x|-2|