Предмет: Математика,
автор: magomedowvad
Под цифрой 2 и 9. Решите п
Приложения:
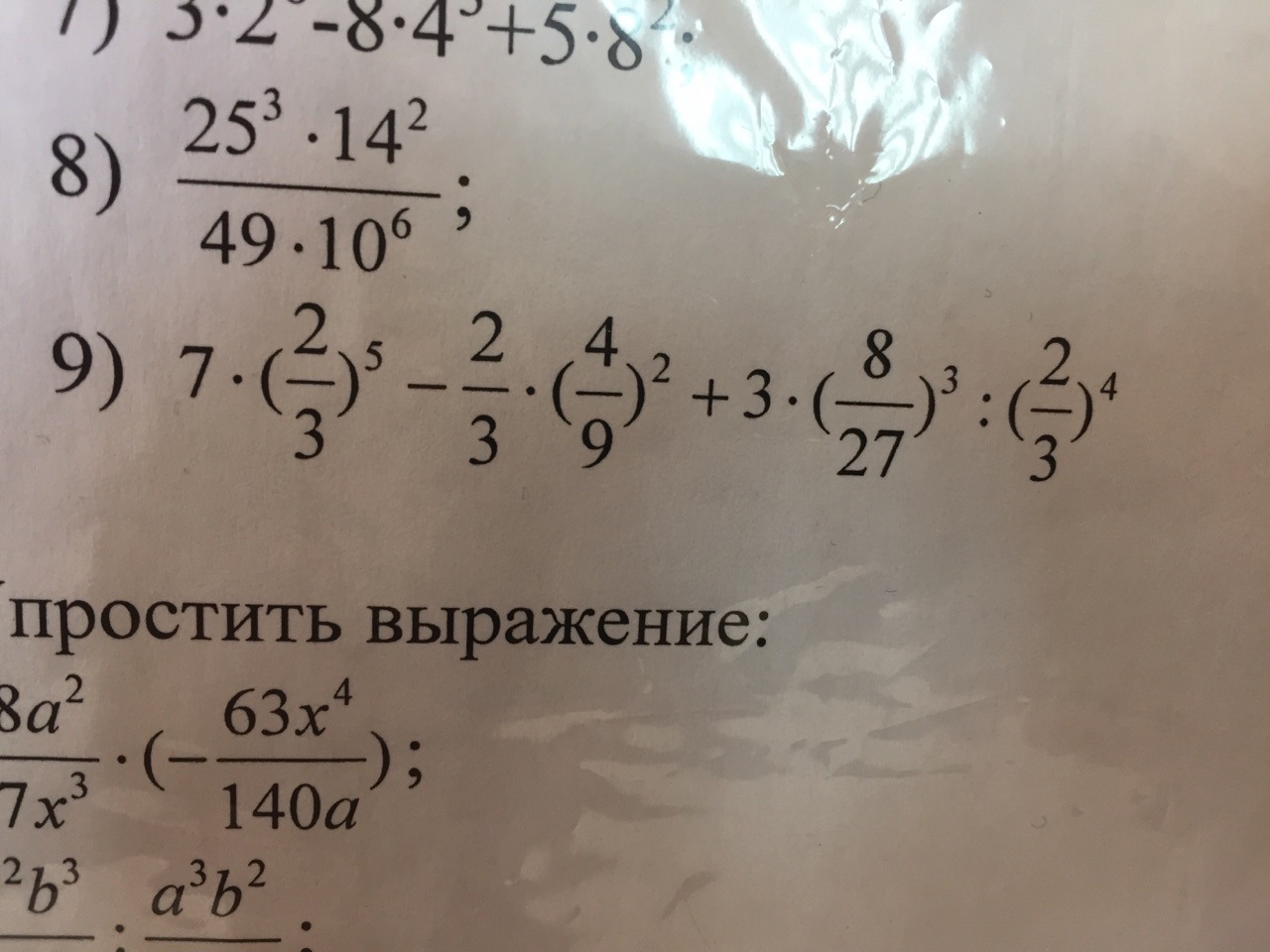
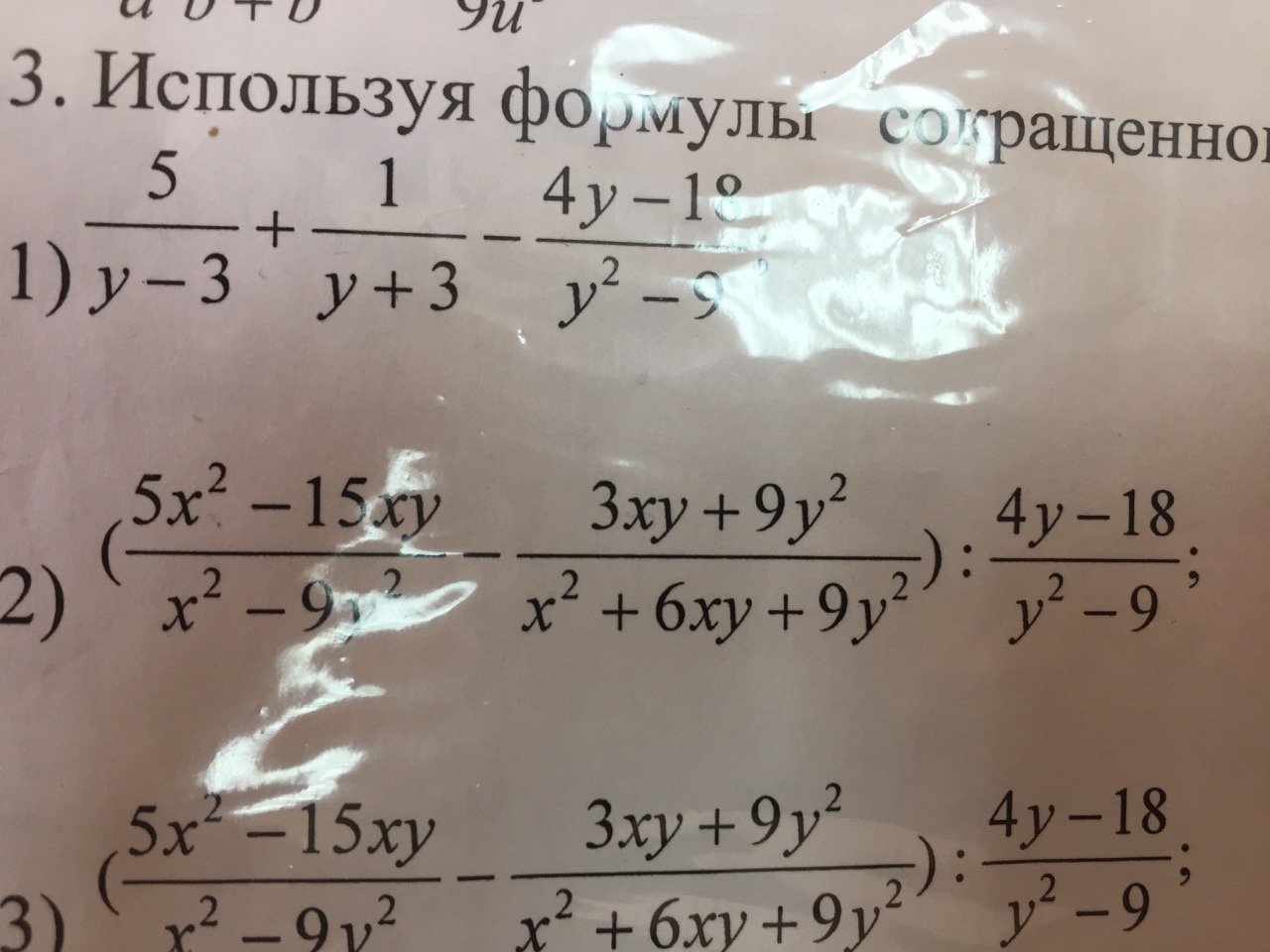
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Химия,
автор: mineko97
Предмет: Русский язык,
автор: Ezkermesazhar25
Предмет: География,
автор: dyshinovas
Предмет: Математика,
автор: bikbaevakatya
Предмет: Математика,
автор: ника908мол