Предмет: Геометрия,
автор: angellike2005
Из вершины прямого угла С прямоугольного треугольника АВС, у которого ∠В=30°, АВ=36 см, проведена высота СН. Найдите длину отрезка НВ
Ответы
Автор ответа:
21
∠ВАС = ∠ВСН = 90° - 30° = 60°
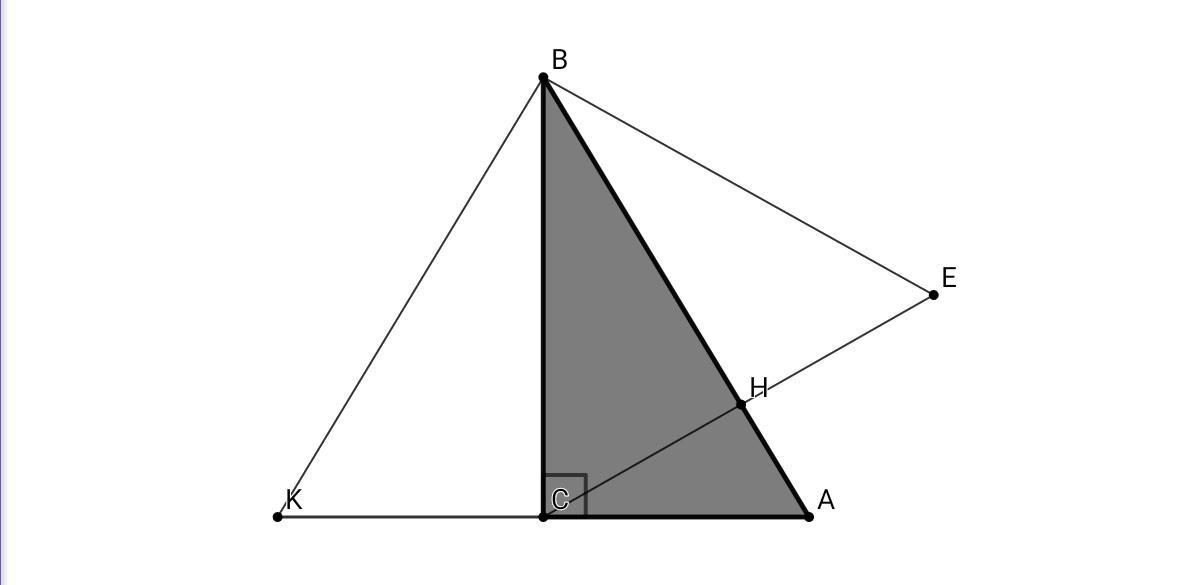
Отобразим ΔАВС относительно ВС, а ΔВСН относительно ВН ⇒ ΔАВК , ΔВСЕ - правильные
Как известно, высота правильного треугольника рассчитывается по формуле: h = a√(3)/2 , где а - сторона треугольника, то есть а = 36 см
ВН - высота правильного треугольника, сторона ВС которого также является высотой правильного треугольника. Значит,
BH = (a√3/2) • (√3/2) = 3a/4 = 3•36/4 = 27 см
ОТВЕТ: 27 см
Приложения:
Автор ответа:
4
Ответ:
27 см
Объяснение:
АВ = 36 см это гипотенузы, углы 30° и 60°, катеты АС=18 см, ВС=18√3 см.
Площадь треугольника это половина произведения катетов.
S = 18*18√3/2 = 162√3
С другой стороны, площадь
S = c*h/2 = AB*CH/2 = 36*CH/2 = 18*CH.
Приравниваем площадь.
S = 18*CH = 162√3
CH = 162√3/18 = 9√3
Получаем прямоугольный треугольник ВСН, у которого катеты СН = 9√3 и неизвестный НВ, а гипотенуза ВС = 18√3 = 2*СН.
Углы опять 30° и 60°.
НВ = ВС*√3/2 = 18√3*√3/2 = 27 см.
Похожие вопросы
Предмет: Английский язык,
автор: ashpinmax
Предмет: Английский язык,
автор: lama333
Предмет: Биология,
автор: Uruswed
Предмет: Химия,
автор: Reevinko
Предмет: Математика,
автор: yashunya72